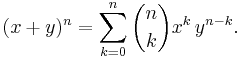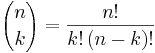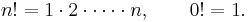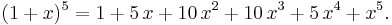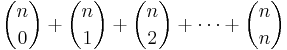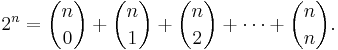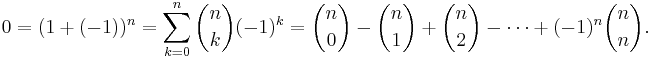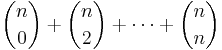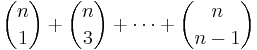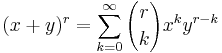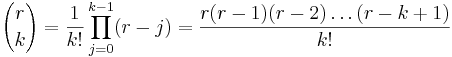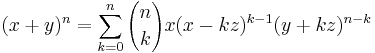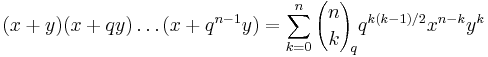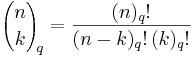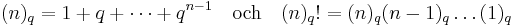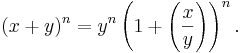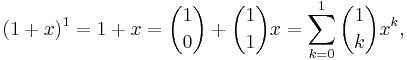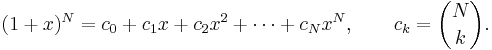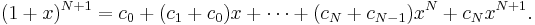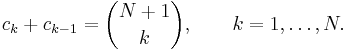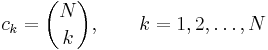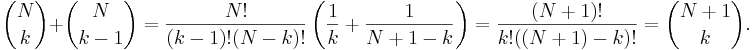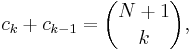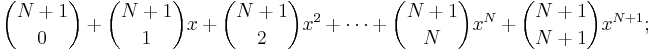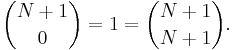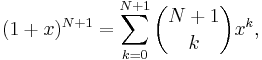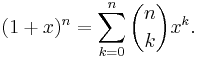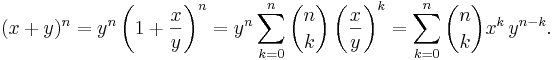Binomialsatsen

Från Rilpedia

Version från den 16 maj 2009 kl. 16.43 av RibotBOT (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Binomialsatsen är en allmän sats inom den matematiska analysen. Satsen används för att utveckla potenser av binom.

Innehåll

Satsens lydelse

Låt x och y vara två godtyckligt valda (reella eller komplexa) tal. För varje naturligt tal n gäller följande exponentiering av binomet x+y\,:
(x + y)^n = \sum_{k=0}^{n} \binom{n}{k} x^k \, y^{n - k}.

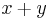Talen

{n \choose k} = \frac{n!}{k!\,(n-k)!}

är binomialkoefficienter (de utläses n över k) och symbolen n! betecknar n-fakultet:

n! = 1 \cdot 2 \cdot \cdots \cdot n, \qquad 0!=1.

Historik

Binomialsatsen och Pascals triangel — som kan användas för att räkna ut koefficienterna — brukar tillskrivas Blaise Pascal som beskrev dem på 1600-talet. De var dock tidigare kända av den kinesiske matematikern Yang Hui på 1200-talet, den persiske matematikern Omar Khayyám på 1000-talet, samt den indiske matematikern Pingala på 200-talet f.Kr.

Tillämpningar av binomialsatsen

  • Binomialsatsen låter oss snabbt skriva upp exponentieringen av binom, som annars skulle vara långtråkiga att utveckla för hand:
Vi illustrerar detta genom att visa hur man snabbt kan utveckla (1 + x)5.
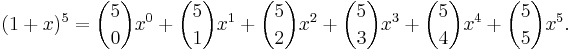
(1+x)^5 = \binom{5}{0}x^0 + \binom{5}{1}x^1 + \binom{5}{2}x^2 + \binom{5}{3}x^3 + \binom{5}{4}x^4 + \binom{5}{5}x^5.
Den femte raden i Pascals triangel innehåller alla binomialkoefficienter som förekommer i denna utveckling: 1, 5, 10, 10, 5 och 1.
Därför kan vi skriva:
(1+x)^5 = 1 + 5\,x + 10 \, x^2 + 10 \, x^3 + 5 \, x^4 + x^5.
  • Om M är en mängd bestående av n stycken element, så anger binomialkoefficienten, 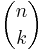\binom{n}{k}, antalet delmängder till M bestående av k stycken element. Med hjälp av binomialsatsen visar man att det går att bilda 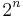2^n\, stycken delmängder till mängden M:
Det finns 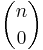\binom{n}{0} stycken delmängder bestående av noll element och 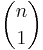\binom{n}{1} stycken delmängder bestående av ett element och 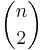\binom{n}{2} stycken delmängder bestående av två element och ... och 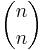\binom{n}{n} stycken delmängder bestående av n element. Totalt finns det
\binom{n}{0} + \binom{n}{1} + \binom{n}{2} + \cdots + \binom{n}{n}
stycken delmängder till mängden M. Binomialsatsen ger — med x = 1 och y = 1 —
2^n = \binom{n}{0} + \binom{n}{1} + \binom{n}{2} + \cdots + \binom{n}{n}.


  • Med hjälp av binomialsatsen kan vi också visa att om man har en mängd bestående av n stycken element, så är antalet delmängder med ett udda antal element lika med antalet delmängder med ett jämnt antal element.
Vi tillämpar bara binomialsatsen för de två talen 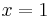x = 1\, och y = -1\,:
0 = (1 + (-1))^n = \sum_{k=0}^n\binom{n}{k}(-1)^k = \binom{n}{0} - \binom{n}{1} + \binom{n}{2} - \cdots + (-1)^n\binom{n}{n}.
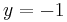Om heltalet n är jämnt finns det
\binom{n}{0} + \binom{n}{2} + \cdots + \binom{n}{n}
stycken delmängder med ett jämnt antal element, och
\binom{n}{1} + \binom{n}{3} + \cdots + \binom{n}{n-1}
stycken delmängder med ett udda antal element. Motsvarande resultat gäller då n är ett udda tal.

Newtons generaliserade binomialsats

Isaac Newton visade att man kan generalisera satsen till att gälla fallet då exponenten inte är ett heltal

(x+y)^r = \sum_{k=0}^\infty {r\choose k} x^k y^{r-k}

där r kan vara ett godtyckligt komplext tal och | x / y | < 1. Binomialkoefficienterna ges då av

{r \choose k} = \frac{1}{k!} \prod_{j=0}^{k-1} (r-j) = \frac{r(r-1)(r-2)\ldots (r-k+1)}{k!}

När k = 0 reduceras denna produkt till en tom produkt och är lika med 1.


Andra generaliseringar

Abel

Niels Henrik Abel generaliserade 1826 binomialsatsen till

(x+y)^n = \sum_{k=0}^n {n\choose k} x(x-kz)^{k-1}(y+kz)^{n-k}

som gäller för 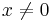x\not=0 och icke-negativa heltal n. Formeln ger den vanliga binomialsatsen när z = 0.

Cauchy

Augustin Louis Cauchy gav 1843 en s.k. q-analog generalisering av binomialsatsen

(x+y)(x+qy)\ldots(x+q^{n-1}y) = \sum_{k=0}^n {n\choose k}_{\!q} q^{k(k-1)/2}x^{n-k}y^k

för icke-negativa heltal n. I ovanstående formel definieras q-binomialkoefficienterna (även kallade gaussiska polynom) av

{n\choose k}_{\!q} = \frac{(n)_q!}{(n-k)_q!\,(k)_q!}

där (n)q och (n)q! är beteckningar för

(n)_q = 1+q+\cdots+q^{n-1}\quad\text{och}\quad (n)_q! = (n)_q(n-1)_q\ldots(1)_q

Bevis av binomialsatsen

Man kan bevisa binomialsatsen via matematisk induktion. Man börjar med att visa att binomialsatsen gäller för det naturliga talet n = 1. Sedan antar man att binomialsatsen är sann för det naturliga talet n = N. Därefter visar man att detta innebär att binomialsatsen är sann för det efterföljande naturliga talet: N + 1. Beviset avslutas sedan genom att åberopa induktionsaxiomet, som låter oss dra slutsatsen att binomialsatsen är sann för varje naturligt tal n.

Vi noterar att det räcker att bevisa satsen då talet y = 1, eftersom

(x + y)^n = y^n\left(1 + \left(\frac{x}{y}\right)\right)^n.

Låt x vara ett godtyckligt valt (reellt eller komplext) tal. För det naturliga talet n = 1 gäller

(1+x)^1 = 1 + x = \binom{1}{0} + \binom{1}{1}x = \sum_{k=0}^1 { 1 \choose k }x^k,

vilket stämmer överens med binomialsatsen.

Antag nu att satsen är sann för det naturliga talet n = N:

(1+x)^N = c_0 + c_1 x + c_2 x^2 + \cdots + c_N x^N, \qquad c_k = \binom{N}{k}.

Detta är det så kallade induktionsantagandet.


För det efterföljande naturliga talet n = N + 1 utvecklar vi potensen (1 + x)n och grupperar koefficienterna:

(1+x)^{N+1} = c_0 + (c_1 + c_0)x + \cdots + (c_N + c_{N-1})x^N + c_N x^{N+1}.

Vi vill visa att en godtycklig koefficient i denna utveckling kan uttryckas som:

c_k + c_{k-1} = \binom{N+1}{k}, \qquad k = 1,\dots,N.
Induktionsantagandet talar om för oss att koefficienten
c_k = \binom{N}{k}, \qquad k = 1, 2, \dots, N
och följande beräkning uttrycker summan 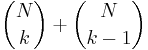\binom{N}{k} + \binom{N}{k-1} som binomialkoefficienten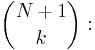 \binom{N+1}{k}:
Definitionerna av binomialkoefficient och fakultet låter oss uttrycka
\binom{N}{k} + \binom{N}{k-1} = \frac{N!}{(k-1)!(N-k)!}\left(\frac{1}{k} + \frac{1}{N+1-k}\right) = \frac{(N+1)!}{k!((N+1)-k)!} = \binom{N+1}{k}.

Följaktligen är koefficienterna ck sådana att

c_k + c_{k-1} = \binom{N+1}{k},

vilket innebär att vi kan uttrycka utvecklingen av potensen (1 + x)N + 1 som:

\binom{N+1}{0} + \binom{N+1}{1}x + \binom{N+1}{2}x^2 + \cdots + \binom{N+1}{N}x^N + \binom{N+1}{N+1}x^{N+1};
här har vi använt oss av det faktum att
\binom{N+1}{0} = 1 = \binom{N+1}{N+1}.

Vi skriver utvecklingen av potensen (1 + x)N + 1 kortfattat med hjälp av summa-symbolen:

(1+x)^{N+1} = \sum_{k=0}^{N+1}\binom{N+1}{k}x^k,

vilket är det resultat som binomialsatsen säger att vi skall få då vi tillämpar den för heltalet N + 1.

Det sista steget i beviset av binomialsatsen är att åberopa induktionsaxiomet, vilket säger att om man kan visa att ett påstående — i detta fall utvecklingen av potensen 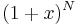(1+x)^N\, — rörande de naturliga talen är sant för det naturliga talet N och att det även är sant för talets efterföjare, N + 1, så är påståendet sant för alla naturliga tal.

Eftersom talet x var godyckligt valt har vi lyckats bevisa följande påstående :

För varje (reellt eller komplext) tal x och för varje naturligt tal n, kan man utveckla potensen 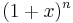(1+x)^n\, enligt:
(1+x)^n = \sum_{k=0}^n\binom{n}{k}x^k.

Vi lägger sista handen vid beviset genom att visa exponentieringen av det generella binomet 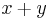x+y\,:

(x+y)^n = y^n\left(1 + \frac{x}{y}\right)^n = y^n\sum_{k=0}^n\binom{n}{k}\left(\frac{x}{y}\right)^k = \sum_{k=0}^n\binom{n}{k}x^k \, y^{n-k}.

Härmed är beviset av binomialsatsen fullbordat.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Binomialsatsen"
Personliga verktyg