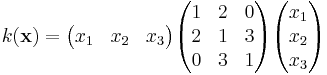Spektralsatsen
Från Rilpedia
Spektralsatsen är en samling matematiska satser inom den matematiska grenen linjär algebra. Satserna säger vilka linjära avbildningar som har en bas av ortonormerade egenvektorer och alltså kan diagonaliseras i denna bas, det vill säga huruvida matrisen A kan uttryckas som A = UDU * , där D är en diagonalmatris och U en unitär matris. Satsen säger dels att vissa matriser är diagonaliserbara, dels att man inte behöver räkna ut en invers, som man behöver vid allmänna diagonaliseringar, då matrisen skrivs A = TDT − 1.
Innehåll |
Spektralsatser
Spektralsatsen finns i flera utföranden. Spektralsatsen för symmetriska avbildningar är oftast den enda som lärs ut i en grundkurs i linjär algebra.
Symmetriska avbildningar
Om V är ett ändligt-dimensionellt reellt euklidiskt rum gäller följande:
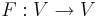 är en symmetrisk linjär avbildning
är en symmetrisk linjär avbildning 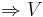 har en ortonormerad bas av egenvektorer till F.
har en ortonormerad bas av egenvektorer till F.
Hermitska avbildningar
Om V är ett ändligt-dimensionellt komplext euklidiskt rum gäller följande:
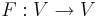 är en hermitsk linjär avbildning
är en hermitsk linjär avbildning 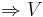 har en ortonormerad bas av egenvektorer till F.
har en ortonormerad bas av egenvektorer till F.
Normala avbildningar
Om V är ett ändligt-dimensionellt komplext euklidiskt rum gäller följande:
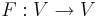 är en normal linjär avbildning
är en normal linjär avbildning 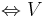 har en ortonormerad bas av egenvektorer till F.
har en ortonormerad bas av egenvektorer till F.
Notera ekvivalensen: Normala linjära avbildningar är alltså exakt de avbildningar som kan diagonaliseras med en bas av ortonormerade egenvektorer.
Bevis
Spektralsatsen bevisas för reella symmetriska avbildningar genom matematisk induktion.
- Visar att satsen gäller inledningsvis. Dimensionen för rummet,
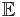 , är då 1.
, är då 1.
Vektorn 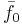 tillhör rummet
tillhör rummet 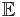 och har längden (beloppet) 1 vilket ger att F:s avbildning av
och har längden (beloppet) 1 vilket ger att F:s avbildning av 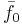 är en multipel av sig själv.
är en multipel av sig själv.
Vektorn 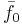 är alltså en egenvektor till F och därmed den sökta basen till rummet.
är alltså en egenvektor till F och därmed den sökta basen till rummet.
- Antar vidare att satsen är sann för rum av dimensionen p, vilket åtminstone stämmer då dimensionen av rummet är 1 (enligt ovan).
Visar då att satsen även är sann för rum av dimensionen p + 1.
Om λ1 är en reell rot till sekularekvationen för F i rummet  och vektorn
och vektorn 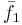 är en egenvektor till F med längden 1. (Vilket är ekvivalent med att F:s avbildning av
är en egenvektor till F med längden 1. (Vilket är ekvivalent med att F:s avbildning av 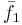 blir
blir 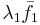 .)
.)
Bildar mängden V som innehåller alla vektorer i 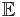 som är ortogonala mot
som är ortogonala mot  . Dimensionen för V blir alltså p.
. Dimensionen för V blir alltså p.
Fyller ut 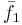 till en ON-bas för
till en ON-bas för 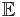 .
.
F:s matris i den basen blir då symmetrisk enligt:  .
.
Vi ser då att då 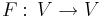 så har V en ortonormerad bas bestående av egenvektorer till F :
så har V en ortonormerad bas bestående av egenvektorer till F :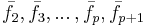 .
.
Det betyder i sin tur att 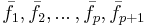 är en ortonormerad bas bestående av egenvektorer till F
är en ortonormerad bas bestående av egenvektorer till F
- Satsen är sann inledningsvis och om den är sann för rum av dimensionen p så är den även sann för rum av dimensionen p + 1. Då är satsen sann i all oändlighet enligt induktionsaxiomet.
Historia
Spektralsatsen utformades under början av 1800-talet av Augustin-Louis Cauchy.
Tillämpningar
Kvadratiska former
En kvadratisk form kan skrivas som en symmetrisk matris, och kan därför diagonaliseras med en ortonormerad bas. Den blir då mer lätthanterlig. Spektralsatsen kan i vissa fall vara formulerad som att en kvadratisk form i ett euklidiskt rum har en kanonisk ortonormerad bas. Detta gör att spektralsatsen kan användas för att ta fram olika andragradsytors huvudaxlar.
Exempelvis kan den kvadratiska formen 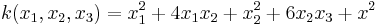 skrivas på matrisform som:
skrivas på matrisform som:
som har egenvärdena 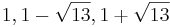 , så att k i den nya basen kan skrivas
, så att k i den nya basen kan skrivas 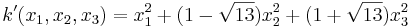 .
.
Referenser
- Janfalk, Ulf, Linjär Algebra, 2007, MAI (Linköpings Universitet)
- Thompson, Jan, Matematiklexikon, 2005, Wahlström & Widstrand
- Treil, Sergei, Linear Algebra Done Wrong, 2004, elektroniskt tillgänglig http://www.math.brown.edu/%7Etreil/papers/LADW/LADW.html