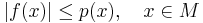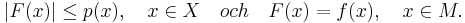Hahn-Banachs sats

Från Rilpedia

Version från den 7 maj 2009 kl. 16.22 av ArthurBot (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Inom den gren av matematiken som kallas funktionalanalys är Hahn-Banachs sats ett ofta använt resultat.

Formulering

Låt f vara en linjär funktional vars definitionsmängd är ett underrum M till ett komplext vektorrum X och låt p vara en semi-norm vars definitionsmängd är vektorrummet X. Om funktionalen är begränsad av semi-normen på underrummet,
\vert f(x)\vert \leq p(x), \quad x \in M
så kan funktionalen utvidgas till en linjär funktional, F, vars definitionsmängd är X, och som är begränsad av semi-normen:
\vert F(x)\vert \leq p(x), \quad x \in X \quad och \quad F(x) = f(x), \quad x \in M.


Beviset av Hahn-Banachs sats är icke-konstruktivt, då det utnyttjar Zorns lemma. Det går emellertid att undvika Zorns lemma för vissa typer av vektorrum, exempelvis då det är ett så kallat Hilbertrum; det är Riesz representationssats som åstadkommer detta. Enligt denna är varje begränsad linjär funktional på ett Hilbertrum detsamma som en inre produkt med avseende på ett till funktionalen associerat element i Hilbertrummet.

Bevis av Hahn-Banachs sats

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Hahn-Banachs_sats"
Personliga verktyg