Delrum
Från Rilpedia
Ett reellt delrum av ett linjärt rum (även linjärt delrum) är en icke tom delmängd M av ett linjärt rum L som uppfyller de vanliga villkoren för linjära rum:
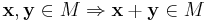
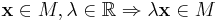 .
.
Komplexa delrum (av komplexa linjära rum) definieras på motsvarande sätt.
Om M1,...,Mn är delrum av L, så definieras summan av dessa delrum som mängden av alla möjliga summor av element i delrummen:
L är en direkt summa av M1,...,Mm om varje element i L kan anges unikt som en summa m1 + ... + mn, där varje 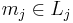 och den betecknas
och den betecknas  .
.
Begreppet delrum inom andra delar av matematiken än linjär algebra
Allmänt är ett delrum M av ett givet rum L en icke-tom delmängd, som har "samma sorts struktur" som L. Detta betyder att om L är normerat, så ska M vara det. Om L är ett metriskt rum, så ska även M vara det och så vidare.
Notera dock att matematiker inte är helt överens när det gäller huruvida en delmängd icke-komplett mängd M kan vara ett delrum av ett komplett rum L. Därigenom kan man i vissa sammanhang se att det finns delrum av Banachrum som är normerade, men inte kompletta, vilket skulle varit fallet om all struktur måste delas av det omgivande rummet och delmängden.
(Detta är ett exempel på en situation då det finns två 'oförenliga' definitioner i bruk, så var försiktig!)