Satsen om den öppna avbildningen
Från Rilpedia
Texten från svenska Wikipedia
Satsen om den öppna avbildningen eller Banach-Schauders sats är inom funktionalanalys ett mycket användbart resultat.
Innehåll |
Banach-Schauders sats
- Låt X och Y vara två Banachrum. Varje kontinuerlig, linjär och surjektiv operator,
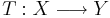, är en öppen avbildning.
Satsens innebörd
En öppen avbildning skall jämföras med en kontinuerlig avbildning:
- En avbildning 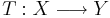är kontinuerlig om den inversa bilden av en öppen mängd är en öppen mängd:
- För varje öppen mängd U i rummet Y är den inversa bilden
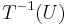en öppen mängd i rummet X.
- För varje öppen mängd U i rummet Y är den inversa bilden
- En avbildning 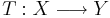är öppen om varje bild av en öppen mängd är en öppen mängd:
- För varje öppen mängd V i rummet X är bilden T(V) en öppen mängd i rummet Y.
Banach-Schauders sats medför att öppna mängder i rummet X svarar mot öppna mängder i rummet Y och vice versa, om X och Y kan förbindas med en avbildning som är kontinuerlig, linjär och bijektiv. Ett annat sätt att uttrycka detta är att säga att de topologiska strukturerna på rummen X och Y är isomorfa och att avbildningen T är en en homeomorfism: Att undersöka kontinuitetsegenskaper i rummet X är detsamma som att undersöka kontinuitet i rummet Y och vice versa.
Bevis av Banach-Schauders sats
Beviset bygger på Baires kategoriteorem och begreppet ingenstans-tät mängd.
