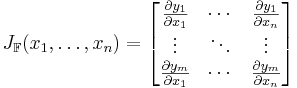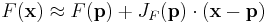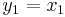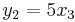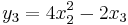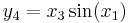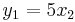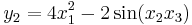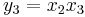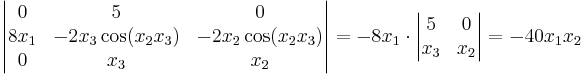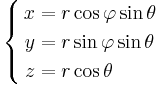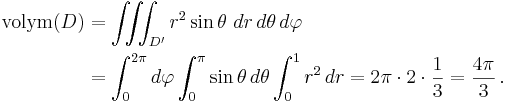Jacobimatris
Från Rilpedia
Jacobimatris (också kallad Jacobian eller funktionalmatris), efter Carl Gustav Jakob Jacobi, är en matris bestående av olika partialderivator som tillhör ett system av funktioner. Tillsammans med dess determinant (jacobideterminanten) används den inom vektoranalysen. Både matrisen och dess determinant kan ibland något slarvigt benämnas jacobian.
Innehåll |
Jakobimatris
Jacobimatrisen är en matris innehållande alla första ordningens partiella derivator för en vektorvärd funktion, och är av betydelse då den representerar den bästa linjäraapproximationen av en differentierbar funktion i en omgivning till en given punkt. Jakobimatrisen kan därmed ses som en motsvarighet till derivata för vektorvärda funktioner.
Låt 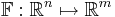 vara en funktion från ett Euklidiskt rum av dimension n till ett Euklidiskt rum av dimension m. En sådan funktion ges av m reella funktioner,
vara en funktion från ett Euklidiskt rum av dimension n till ett Euklidiskt rum av dimension m. En sådan funktion ges av m reella funktioner,  . Om de existerar kan de partiella derivatorna av dessa funktioner ordnas i en
. Om de existerar kan de partiella derivatorna av dessa funktioner ordnas i en 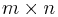 -matris, alltså
-matris, alltså 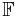 Jacobimatris
Jacobimatris 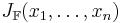 , enligt:
, enligt:
Ett alternativt skrivsätt är 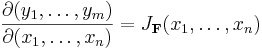
Matrisens i:e rad ges alltså av gradienten till yi.
Om p är en punkt i  och
och 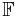 är differentierbar i p, så ges dess derivata av
är differentierbar i p, så ges dess derivata av 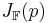 . Här kommer den linjära transformation som beskrivs av
. Här kommer den linjära transformation som beskrivs av 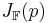 vara den bästa möjliga approximationen av
vara den bästa möjliga approximationen av 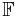 i en omgivning till p, i meningen att
i en omgivning till p, i meningen att
för x nära p.
Exempel
Följande funktion betecknar ett variabelbyte från sfäriska koordinater till kartesiska koordinater:
![\mathbb{F}: \R^+ \times [0,2\pi)\times [0,\pi]\mapsto \R^3](/w/images/sv.rilpedia.org/math/b/0/2/b028871bcd68bc28413e04b5849f7e8d.png) .
.
Mer explicit skrivs den
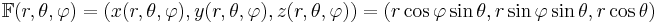 .
.
Jacobimatrisen för detta variabelbyte är
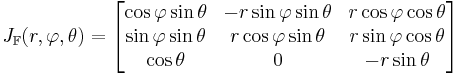 .
.
Jacobimatrisen för funktionen 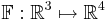 med komponenter
med komponenter
är
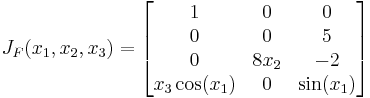 ,
,
vilket visar att jacobimatrisen inte behöver vara kvadratisk.
Jakobideterminanten
Om m = n, det vill säga 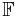 är en funktion från ett n-dimensionellt rum till ett annat n-dimensionellt rum, så är Jacobimatrisen kvadratisk, och därmed är dess determinant väldefinierad. Denna kallas jacobideterminanten, och dess värde i en punkt ger viktig information om funktionen i denna omgivning. Om
är en funktion från ett n-dimensionellt rum till ett annat n-dimensionellt rum, så är Jacobimatrisen kvadratisk, och därmed är dess determinant väldefinierad. Denna kallas jacobideterminanten, och dess värde i en punkt ger viktig information om funktionen i denna omgivning. Om 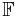 är kontinuerligt differentierbar är den även inverterbar i närheten av p om Jacobideterminanten är nollskild i p. Om determinanten är positiv i p bevarar
är kontinuerligt differentierbar är den även inverterbar i närheten av p om Jacobideterminanten är nollskild i p. Om determinanten är positiv i p bevarar 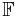 orientering, och om den är negativ skiftar
orientering, och om den är negativ skiftar 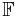 orientering. Vidare ger absolutvärdet av Jacobideterminanten i p den faktor med vilken
orientering. Vidare ger absolutvärdet av Jacobideterminanten i p den faktor med vilken 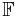 skalar om area/volym/hypervolym i närheten av p. Detta används i variabelsubstitution.
skalar om area/volym/hypervolym i närheten av p. Detta används i variabelsubstitution.
Exempel
Jakobideterminanten för funktionen 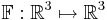
med komponenterna
är
Vi kan av detta dra slutsatsen att 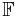 kastar om orienteringen i närheten av alla punkter där x1 och x2 har samma tecken, och att funktionen är lokalt inverterbar överallt utom i x1 = 0 eller x2 = 0. Ett litet objekt som befinner sig i närheten av (1,1,1) som mappas om av
kastar om orienteringen i närheten av alla punkter där x1 och x2 har samma tecken, och att funktionen är lokalt inverterbar överallt utom i x1 = 0 eller x2 = 0. Ett litet objekt som befinner sig i närheten av (1,1,1) som mappas om av 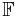 kommer öka sin volym cirka 40 gånger.
kommer öka sin volym cirka 40 gånger.
Användningar
Jakobideterminanten används när man gör variabelbyten när man integrerar en funktion för att kompensera för basbytet. Den kommer då dyka upp som en multiplikativ term under integraltecknet. Det är vanligtvis nödvändigt att variabelbytet är injektivt, vilket gör att jakobideterminanten är väldefinierad.
Exempel
Följande demonstrerar en användning av jakobideterminanten vid beräkning av en integral. Antag att man vill beräkna volymen av enhetssfären x2 + y2 + z2 = 1. Låt 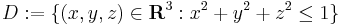 . Volym av D ges då av uttrycket
. Volym av D ges då av uttrycket
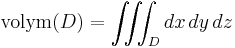 .
.
Görs ett variabelbyte till sfäriska koordinater enligt
transformeras volymelementet dx dy dz till
och området D beskrivs i de nya koordinaterna som
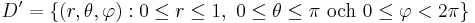 .
.
Strikt sett är detta koordinatbyte inte injektivt i hela D, men om vi exkluderar linjen x = y = 0 får vi ett område med samma volym som D där koordinatbytet är injektivt och vi kan tillämpa koordinatbytet i volymintegralen. Volymintegralen blir därför