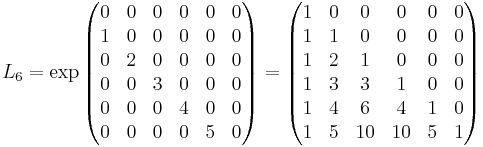Pascalmatris

Från Rilpedia

Texten från svenska Wikipedia

Pascalmatris är inom matematiken en oändlig matris innehållande binomialkoefficienter, liknande Pascals triangel. Pascalmatriser kan uttryckas på tre olika sätt; som höger- eller vänstertriangulära matriser eller som en symmetrisk matris. Om man begränsar Pascalmatrisen till en matris av format 5×5 får man då dessa representationer:

Högertriangulär: 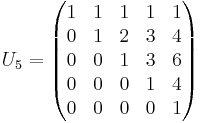$U_5=\begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 2 & 3 & 4 \\ 0 & 0 & 1 & 3 & 6 \\ 0 & 0 & 0 & 1 & 4 \\ 0 & 0 & 0 & 0 & 1 \end{pmatrix}\,\,\,$ Vänstertriangulär: 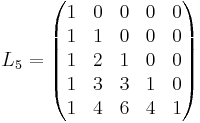$L_5=\begin{pmatrix} 1 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 \\ 1 & 2 & 1 & 0 & 0 \\ 1 & 3 & 3 & 1 & 0 \\ 1 & 4 & 6 & 4 & 1 \end{pmatrix}\,\,\,$ Symmetrisk: $S_5=\begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 1 & 2 & 3 & 4 & 5 \\ 1 & 3 & 6 & 10 & 15 \\ 1 & 4 & 10 & 20 & 35 \\ 1 & 5 & 15 & 35 & 70 \end{pmatrix}.$

Matrisen $S n$ är helt enkelt en matris där kolonnerna är kolonnerna i Pascals triangel, men första elementet i en kolonn är det första nollskilda elementet i triangeln för motsvarande kolonn.

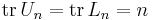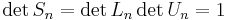Man kan visa att $S n = L n U n$ , se att spåret av de två första matriserna är: $\operatorname{tr}\, U_n = \operatorname{tr}\, L_n = n \,$ , samt att $\det S_n = \det L_n \det U_n = 1\,$ .

Man kan också se att 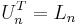$U_n^T = L_n$ , där $T$ står för transponat.

Konstruktion

Pascalmatriser kan fås genom att ta matrisexponentialen av en speciell matris med särskilda element antingen i diagonalen över eller under huvuddiagonalen och nollor på alla andra platser, där elementet på rad $k$ är $k$ . Exempel:

$L_6 = \exp \begin{pmatrix} 0 & 0 & 0 & 0 &0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 & 0 \\ 0 & 0 & 3 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 & 0 \\ 0 & 0 & 0 & 0 & 5 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 \\ 1 & 2 & 1 & 0 & 0 & 0 \\ 1 & 3 & 3 & 1 & 0 & 0 \\ 1 & 4 & 6 & 4 & 1 & 0 \\ 1 & 5 & 10 & 10 & 5 & 1 \end{pmatrix}$

och $U 6$ konstrueras likartat, men matrisen som man utgår ifrån har elementen i superdiagonalen. Man kan sedan konstruera $S 6 = L 6 U 6$ . Konstruktionen gäller för alla $n$ , observera dock att $e A e B = e A B$ i allmänhet inte gäller då $A, B$ är matriser, så man måste räkna ut två matrisexponentialer om man vill veta $S n$ , eller utnyttja att 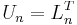$U_n = L_n^T$ .

Pascalmatris

Från Rilpedia

Konstruktion

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk