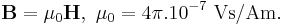Magnetfält
Från Rilpedia
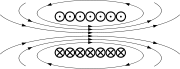
Inom fysiken behandlas magnetiska fält som vektorfält, vilka beskriver krafterna mellan magneter och strömförande elektriska ledare. Vektorfält kan åskådliggöras med hjälp av pilar av olika längd och riktning eller med fältlinjer, där fältstyrkan är proportionell mot linjetätheten. Magnetiska fält kan experimentellt synliggöras med hjälp av järnfilspån, vilka ställer in sig i fältlinjernas riktning.
Innehåll |
Enhetssystem för magnetism
Det finns inom magnetismen olika enhetssystem och konventioner vilket kan te sig förvirrande. Maxwells ekvationer skulle se enklare ut i ett system av enheter där ε0 = μ0 = 1 så att även ljusets hastighet är = 1, men detta ger opraktiska enheter för elektrisk spänning och strömstyrka. Denna artikel använder SI-enheter.
B-fältet (flödestäthet)
B-fältet, magnetisk flödestäthet, är ett av två sätt att betrakta magnetfält (det andra sättet är H-fältet). B-fältet mäts i SI-enheten tesla (T = Wb/m²) eller i cgs-enheten gauss (1 T = 10 000 Gauss). Tesla (T) är en förhållandevis stor enhet. Elektromagneter med järnkärna kan bara åstadkomma fält på någon tesla. Ofta använder man µT (mikrotesla, en miljondels tesla). Jordens magnetfält har styrkan 50 till 100 µT (0,5 gauss till 1 gauss).
Det magnetiska flödet (ofta betecknat med en stor grekisk bokstav fi Φ) mäts i SI-systemet i Weber = volt·sekund.
H-fältet (fältstyrka)
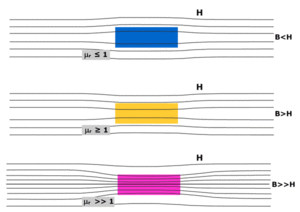
H-fältet, magnetisk fältstyrka, är det andra sättet att betrakta magnetfält. H-fältet mäts i A/m och ses som orsakad av fria strömmar, medan B är orsakad av både elektriska strömmar och magnetiska ämnens magnetisering. I vakuum finns ingen magnetisering och därför gäller i SI-systemet
Värdet av den magnetiska konstanten μ0 (i vakuum lika med permeabiliteten μ) är genom Ampères lag en följd av enheten amperes definition.
Magnetisering
Det finns inom SI två sätt att ta med magnetiska fält orsakad av material. Enligt det ena sättet betraktar man ämnets magnetisering som orsakad av hypotetiska amperska strömmar (motsats till fria strömmar). Så får man B = μ0 (H + M), där magnetiseringen ges i samma enheter som H-fältet: A/m. När magnetiseringen betraktas som proportionell mot de fria strömmarnas fält, kan man skriva B = μ H = μr μ0 H, där μr är ämnets relativa magnetiska permeabilitet. I mjuka ferromagnetiska material kan μr vara av storleksordningen 10³ eller större. I paramagnetiska och diamagnetiska material är magnetiseringen liten. Där brukar man räkna med magnetisk susceptibilitet χ där M = χ H, så att μr = 1 + χ. Diamagnetiska ämnens susceptibilitet är negativ, av storleksordning -10-6. Även i paramagnetiska matarial är χ liten, men positiv.
Det andra sättet räknar med storheten intensitet av magnetisering, betecknad med vektorfältet I. Här gäller B = μ0 H + I. Man ser att I har enheten tesla. Det här sättet är vanligt när man beskriver ferromagnetiska material, där mättnadsmagnetisering ofta ges i tesla. Så har till exempel järn en maximal magnetiseringsintensitet på 2,1 T.
Förening med elektriskt fält
Ørsted, Faraday och Maxwell visade experimentellt och teoretiskt att magnetiska och elektriska fält betingar varandra och kan beskrivas av det elektromagnetiska fältet som är en förening av de magnetiska och elektriska fälten. Elektromagnetisk strålning kan behandlas inom ramen för detta elektromagnetiska fält.
Albert Einsteins arbete i form av den speciella relativitetsteorin ledde till att de magnetiska och elektriska fälten kunde beskrivas av ett elektromagnetiskt tensorfält som är invariant under Lorentztransformationen. Detta innebär bland annat att medan de elektriska och magnetiska fältkomponenterna kan variera mellan olika inertialsystem är den totala Lorentzkraften som verkar på en viss laddning invariant under dessa transformationer. Detta kan anses vara det andra steget i föreningen av de magnetiska och elektriska fälten.
|
|||||||||||