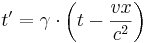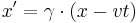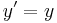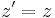Lorentztransformation
Från Rilpedia
Lorentztransformationen är en uppsättning ekvationer inom relativitetsteorin som anger hur tids- och rumskoordinater mäts i olika inertialsystem. Dessa ekvationer används för att transformera dessa storheter mellan olika intertialsystem. En storhet som inte ändras av en Lorentztransformation sägs vara Lorentzinvariant.
Relativitetsteorin postulerar att ljusets hastighet är densamma i alla referenssystem, vilket är ett tillräckligt antagande för att härleda Lorentztransformationen.
Transformationen relaterar rumtidskoordinaterna i två olika inertialsystem S och S' som rör sig i förhållande till varandra. Antag att S' rör sig med hastigheten v längs x-axeln, och att en händelse äger rum vid tiden t och koordinaterna (x,y,z) i systemet S och vid t' och (x',y',z') i systemet S'. Då ges t' och (x',y',z') enligt Lorentztransformationen av
där
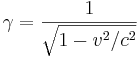 och c är ljushastigheten i vakuum.
och c är ljushastigheten i vakuum.
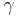 som funktion av
som funktion av 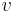 , där
, där 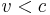 och
och 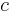 är ca 300000 km/s
är ca 300000 km/sLorentztransformationen ger effekter som tidsdilatation och längdkontraktion, det vill säga att man mäter olika längder och tidsintervall i olika inertialsystem:
- Tidsdilatation:
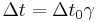
- Längdkontraktion:
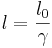
Där "referensvärderna" (till exempel Δt0) avser de värden som en rörlig observatör i referenssystemet skulle mäta dessa värden till.
Dessa fenomen uppfattas inte vid vardagliga hastigheter utan blir väsentliga först vid hastigheter av ungefär 10% av ljusets hastighet i vakuum.
Ekvationerna ger till exempel att ett föremål som färdas i 90% av ljusets hastighet är endast 44% av sin längd i rörelseriktningen, jämfört med när föremålet är i vila. Tidsdilatationen har dock observerats experimentellt, till exempel hos myoner i kosmisk strålning som har för kort livslängd för att kunna nå jordytan om inte tidsdilatationen existerade.
Lorentztransformationen illustreras i romanen Orbitsville av Bob Shaw.