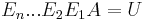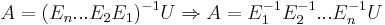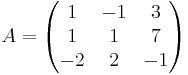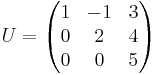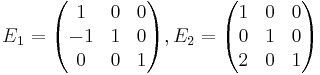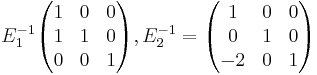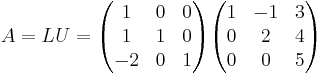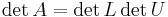LU-faktorisering

Från Rilpedia

(Omdirigerad från LR-faktorisering)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Inom linjär algebra är LU-faktorisering, ibland kallat LR-faktorisering, en matrisfaktorisering där man delar upp en matris i en uppåt triangulär matris (om ursprungsmatrisen är kvadratisk) och en nedåt triangulär matris. LU-faktorisering används för att lösa linjära ekvationsystem med samma vänsterled snabbare.

Innehåll

Definition

För en matris A är LU-faktoriseringen:

A = LU

Om A är kvadratisk är även L (som blir en nedåt triangulär matris) och U (som blir en uppåt triangulär matris) kvadratiska . Om A inte är kvadratisk blir inte U kvadratisk (och då inte heller triangulär), men L blir kvadratisk (och triangulär).

Ibland används en permutationsmatris P för att undvika fel på grund av den numeriska metoden, detta kallas (partiell) pivotering. Matrisen skrivs då om på formen PA = LR

Beräkning

Med elementära matriser

Genom multiplikation med elementära matriser för radadditioner kan den kvadratiska matrisen A omvandlas till en uppåt triangulär matris U (i grund och botten samma sak som Gausselimination). Vi har alltså att:

E_n...E_2E_1A = U \,

Där Ek är en elementär matris. Detta ger att:

A = (E_n...E_2E_1)^{-1}U \Rightarrow A = E_1^{-1}E_2^{-1}...E_n^{-1}U

Då inversen till elementära matriser är lättberäknade (se artikeln om elementära matriser), och alla Ek kan uttryckas som nedåt triangulära matriser (och då även deras inverser), blir produkten av alla Ek en nedåt triangulär matris. Och alltså har A uttryckts som produkten av en uppåt och en nedåt triangulär matris.

Exempel

Följande matris ska LU-faktoriseras:

A = \begin{pmatrix} 1 & -1 & 3 \\ 1 & 1 & 7 \\ -2 & 2 & -1 \end{pmatrix}

Genom Gausselimination ser vi att en uppåt triangulär matris U kan fås genom radadditioner:

U = \begin{pmatrix} 1 & -1 & 3 \\ 0 & 2 & 4 \\ 0 & 0 & 5 \end{pmatrix}

Dessa radoperationer kan beskrivas som:

  1. Dra 1 av rad 1 från rad 2
  2. Lägg 2 av rad 1 till rad 3

Där varje kan uttryckas som en elementär matris:

E_1 = \begin{pmatrix} 1 & 0 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} ,E_2 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 2 & 0 & 1 \end{pmatrix}

Som ger inverser:

E_1^{-1} \begin{pmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} ,E_2^{-1} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -2 & 0 & 1 \end{pmatrix}

Observera hur enkel inversberäkningen är, det är bara att byta tecken på talet utanför diagonalen. Nu kan vi beräkna vårt L:

L = E_2^{-1} E_1^{-1} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -2 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ -2 & 0 & 1 \end{pmatrix}

Observera att ordningen på matriserna kastas om när man tar invers, 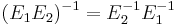(E_1 E_2)^{-1} = E_2^{-1} E_1^{-1} .

A är nu LU-faktoriserad:

A = LU = \begin{pmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ -2 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & -1 & 3 \\ 0 & 2 & 4 \\ 0 & 0 & 5 \end{pmatrix}

Tillämpningar

Ekvationssystemlösning

Om man har en samling ekvationsystem 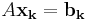A\mathbf{x_k} = \mathbf{b_k} där man vill hitta 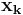\mathbf{x_k} till respektive 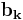\mathbf{b_k} , men A är samma i alla ekvationsystemen, lönar det sig att LU-faktorisera, då man löser ekvationssystemet för en av de triangulära matriserna i taget, det går till som så att man löser ekvationsystemet 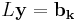L\mathbf{y} = \mathbf{b_k} och sedan ekvationsystemet 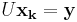U\mathbf{x_k} = \mathbf{y} . Båda dessa ekvationsystem är lätta att lösa då vänsterledet representeras av en triangulär matris.

Inversberäkning

Då A = LU är A − 1 = U − 1L − 1. En triangulär matris är lättare att invertera än en icke-triangulär matris, så det är lättare att beräkna inversen genom LU-faktorisering. Datorprogram beräknar ofta matrisinverser genom LU-faktorisering.

Determinantberäkning

Determinantberäkning är väldigt enkelt för en LU-faktoriserad matris, då determinanten för en triangulär matris är produkten av diagonalelementen och:

\det{A} = \det{L}\det{U}\,

Om L dessutom endast har ettor i diagonalen (som den ofta har, se t.ex. beräkningsexemplet ovan), får vi att:

\det{A} = \det{U} = \prod_{i = 1}^n u_{ii}

Se även

Hämtad från "https://sv.rilpedia.org/wiki/LU-faktorisering"
Personliga verktyg