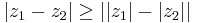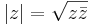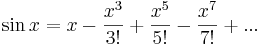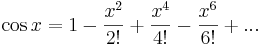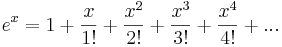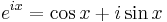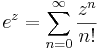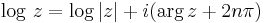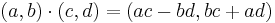Komplexa tal
Från Rilpedia
De komplexa talen är en talmängd som kan ses som en utvidgning av de reella talen. Ett komplext tal kan skrivas som
där det reella talet 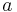 är realdelen,
är realdelen,
det reella talet 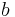 är imaginärdelen
är imaginärdelen
och 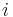 är den imaginära enheten som definieras av
är den imaginära enheten som definieras av
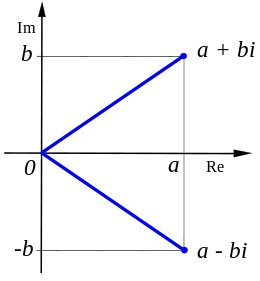
Denna framställning av ett komplext tal kallas också rektangulär form.
Konjugatet 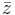 till ett komplext tal
till ett komplext tal 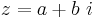 definieras som
definieras som
Enligt Eulers formel gäller
vilket innebär att ett allmänt komplext tal kan skrivas som
där 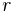 (absolutbeloppet) är avståndet till origo i det komplexa talplanet och
(absolutbeloppet) är avståndet till origo i det komplexa talplanet och 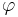 är vinkeln mellan den reella axeln och en linje genom origo och talets punkt i det komplexa talplanet.
är vinkeln mellan den reella axeln och en linje genom origo och talets punkt i det komplexa talplanet.
Absolutbeloppet av ett komplext tal definieras som
Vinkeln 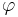 kallas argumentet för
kallas argumentet för 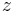 och kan skrivas som
och kan skrivas som
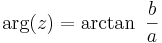 om
om 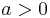 .
.
Denna framställning kallas polär form.
Om b ≠ 0 så är z ett icke reellt komplext tal (till exempel 2 + 4i), och om a = 0 kallas talet rent imaginärt (t.ex 4i).
Mängden av komplexa tal betecknas med 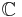 och i äldre litteratur används ofta beteckningen
och i äldre litteratur används ofta beteckningen 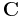 .
.
Innehåll |
Räkneregler
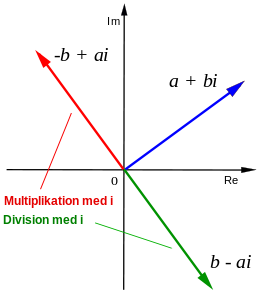
Rektangulär form
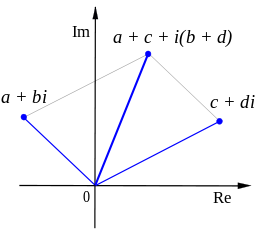
Addition, subtraktion och multiplikation är definierade för de komplexa talen:
Även division kan utföras:
Polär form
Om vi antar att 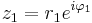 och
och 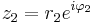 så gäller enligt räknereglerna för exponentiella tal
så gäller enligt räknereglerna för exponentiella tal
Av detta följer
Relationer
Följande relationer gäller för de komplexa talens absolutbelopp:
Övrigt
För beräkningar utförda för hand är det lämpligt att använda den rektangulära formen för addition och subtraktion och den polära formen för multiplikation och division.
Serieutveckling
Enligt de kända serieutvecklingarna för reella 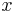 av
av
framgår att exponentialfunktionen 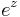 för komplexa
för komplexa 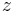 enligt
enligt
kan definieras genom serien
Serien är konvergent för alla 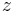 .
.
Logaritmfunktionen
Även den komplexa logaritmen kan definieras och är en flervärd funktion.
Den komplexa logaritmen definieras som
och de flesta logaritmlagar som gäller för de reella talen gäller också för den komplexa logaritmen.
Med hjälp av logaritmfunktionen kan till exempel roten av komplexa tal bildas då
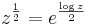 , vilket lätt kan beräknas.
, vilket lätt kan beräknas.
Observera att med denna definition, erhålls två lösningar även när 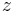 är ett reellt tal.
är ett reellt tal.
Definition
Mängden av komplexa tal 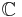 definieras som mängden av ordnade reella talpar
definieras som mängden av ordnade reella talpar 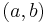 , där
, där 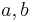 tillhör den reella talmängden, tillsammans med operatorerna + och · för vilka gäller:
tillhör den reella talmängden, tillsammans med operatorerna + och · för vilka gäller:
Definierade på detta sätt utgör 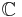 en algebraisk struktur som benämns kropp (vilket bland annat innebär att både addition och multiplikation är tillåtna operationer då de inte leder utanför talmängden).
en algebraisk struktur som benämns kropp (vilket bland annat innebär att både addition och multiplikation är tillåtna operationer då de inte leder utanför talmängden).
De reella talen är komplexa tal av typen 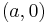 , och den imaginära enheten
, och den imaginära enheten 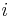 är det komplexa talet
är det komplexa talet 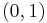 . Alla tal
. Alla tal 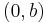 , det vill säga alla tal
, det vill säga alla tal 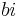 , sägs vara rent imaginära.
, sägs vara rent imaginära.
Det komplexa talplanet, som innehåller mängden 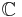 , kallas också för Arganddiagram.
, kallas också för Arganddiagram.
Användningsområden
Komplexa tal är grundläggande för delar av matematiken. Enligt Algebrans fundamentalsats har en ekvation av typen p(x) = 0, där p är ett polynom av graden n, exakt n komplexa rötter. Detta medför att de komplexa talen utgör en algebraiskt sluten kropp. Om p endast har reella koefficienter, och x är en rot till p(x) = 0, så är även konjugatet till x en rot.
Komplexa tal inom fysiken
Komplexa tal är mycket användbara inom fysiken, till exempel för att beskriva vågrörelser eller svängningar inom elektromagnetismen. Detta på grund av att man med komplexa tal samtidigt hanterar både absolutbelopp och fasvinkel, vilket är till stor nytta för att beräkna belopp och fasförskjutningar för spänningar och strömmar.
Med J-omega-metoden behandlas växelströmsproblem i nära analogi med motsvarande likströmsproblem genom införande av komplexa impedanser.
Inom elektrotekniken används ofta komplexa tal i olika slag av transformer, som till exempel Fouriertransformen och Laplacetransformen, för att underlätta vid beräkningar av växelströmsförlopp.
Inom kvantmekaniken är de grundläggande vågfunktionerna komplexa.
I strömningsmekanik används komplexa funktioner för konforma avbildningar.
Historiskt
| En eller flera användare anser att denna text bör infogas i Imaginära tal. (Diskussion) |
Under 1500-talet förekom kvadratrötter ur negativa tal i de lösningar till tredje- och fjärdegradsekvationer som upptäcktes av de italienska matematikerna Niccolo Fontana Tartaglia och Gerolamo Cardano. Även om man bara var intresserade av reella lösningar, ledde dessa formler ibland till sådana kvadratrötter som mellanresultat.
Namnet imaginära för sådana tal myntades av René Descartes på 1600-talet och man betraktade dem länge med stor misstänksamhet. Komplexa tal accepterades först efter att deras geometriska tolkning hade beskrivits och publicerats av Caspar Wessel 1799. Denna beskrivning återupptäcktes flera år senare av bland andra Carl Friedrich Gauss. Den moderna definitionen som ett par av reella tal infördes under 1800-talet av William Rowan Hamilton.
Flera av Leonhard Eulers mest betydande upptäckter vilar väsentligt på införande av komplexa tal. Abels skapelse, de elliptiska funktionerna, förde än mer de komplexa talen i förgrunden inom matematisk forskning. Så blev ytterligare fallet, när den moderna funktionsteorin framväxte ur Abels, Cauchy, Weierstrass' och Riemanns arbeten.
Carl Friedrich Gauss och Karl Weierstrass arbeten har visat, att införande av högre komplexa tal, bildade av flera än två grundenheter, inte medför fördelar jämförliga med dem som vinns genom införande av de av två grundenheter bildade komplexa talen.
Se även
Externa länkar
Källor
- Complex Analysis for Mathematics and Engineering av John H. Mathews & Russel W. Howell
Olika typer av matematiska tal
Naturliga tal - Heltal - Positiva tal - Noll - Negativa tal - Rationella tal - Irrationella tal - Reella tal - Algebraiska tal - Transcendent tal - Imaginära tal - Komplexa tal - Hyperkomplexa tal (Kvaternioner Oktonioner Sedenioner) - Perfekta tal
 Denna artikel är helt eller delvis baserad på material från Nordisk familjebok, 1904–1926 (Not).
Denna artikel är helt eller delvis baserad på material från Nordisk familjebok, 1904–1926 (Not).


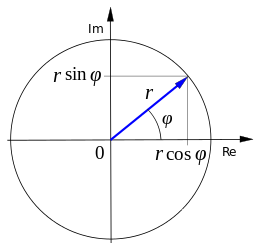
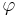 är talets argument
är talets argument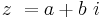
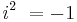
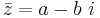
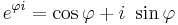
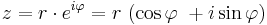
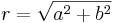


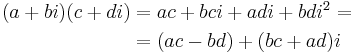
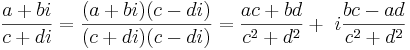
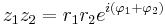
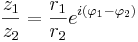
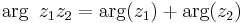
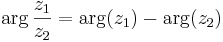
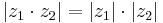
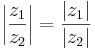
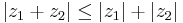 (
(