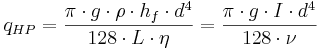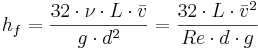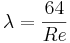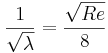Hagen-Poiseuilles lag

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Merge arrows
 Det har föreslagits att denna artikel bör slås ihop med Poiseuilles lag. (Diskutera)

Hagen-Poiseuilles lag för laminär ströming i cirkulärt fullgående ledningar gäller bara i Strömningstillstånd 1 där Reynolds tal (Re) är mindre än ca 2300. Ekvationen, som är uppkallad efter Gotthilf Heinrich Ludwig Hagen och Jean Marie Louis Poiseuille lyder:


q_{HP} = \dfrac {\pi \cdot g \cdot \rho \cdot h_f \cdot d^4}{128 \cdot L \cdot \eta} = \dfrac {\pi \cdot g \cdot I \cdot d^4}{128 \cdot \nu}

och

h_f = \dfrac {32 \cdot \nu \cdot L \cdot \bar v}{g \cdot d^2} = \dfrac {32 \cdot L \cdot \bar v^2}{Re \cdot d \cdot g}

där

qHP = Flöde (m3/s)

π = Matematisk konstant (3,14159...)

g = Tyngdacceleration (m/s2)

ρ = Densitet (kg/m3)

Hf = Strömningsförlust (meter vattenpelare)

d = Ledningens innerdiameter (m)

L = Ledningens längd (m)

η = Dynamisk viskositet (Pa*s)

I = Fall (-)

ν = Kinematisk viskositet (m2/s)

Fil:Del.gif = Medelhastighet (m/s)

Re = Reynolds tal (-)


För friktionstalet (λ), som används i Darcy-Weisbachs ekvation, gäller då följande samband:

\lambda = \dfrac {64}{Re}

och

\dfrac {1}{\sqrt {\lambda}} = \dfrac {\sqrt {Re}}{8}

där

λ = Friktionstal (-)

Re = Reynolds tal (-)


Se även

Hämtad från "https://sv.rilpedia.org/wiki/Hagen-Poiseuilles_lag"
Personliga verktyg