Nikuradse-Prandtls formel

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Nikuradse-Prandtls formel gäller vid turbulent strömning under hydrauliskt råa förhållanden. Formen är namngiven efter Johann Nikuradse och Ludwig Prandtl.

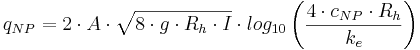q_{NP} = 2 \cdot A \cdot \sqrt {8 \cdot g \cdot R_h \cdot I} \cdot log_{10} \left( \dfrac {4 \cdot c_{NP} \cdot R_h}{k_e} \right) Allmän formel


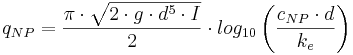q_{NP} = \dfrac {\pi \cdot \sqrt {2 \cdot g \cdot d^5 \cdot I}}{2} \cdot log_{10} \left( \dfrac {c_{NP} \cdot d}{k_e} \right) För cirkulärt fullgående rör

där

qNP = Flöde (m3)

A = Våt tvärsnittsarea (m2)

g = Tyngdacceleration (m/s2)

Rh = Hydraulisk radie (m)

I = Fall (-)

cNP Empirisk konstant (3,71)

Ke = Ekvivalent sandråhet (m)

π = Matematisk konstant (3,14159...)

d = Innerdiameter (m)


Friktionstal

Nikuradse-Prandtls formel kan även användas för att beräkna friktionstalet i Darcy-Weisbachs ekvation, varpå formeln får följande utseende:

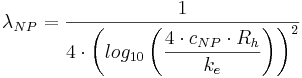\lambda_{NP} = \dfrac {1}{4 \cdot \left( log_{10} \left( \dfrac {4 \cdot c_{NP} \cdot R_h}{k_e} \right) \right) ^2 } Allmän formel


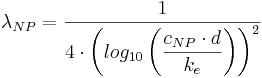\lambda_{NP} = \dfrac {1} {4 \cdot \left( log_{10} \left( \dfrac {c_{NP} \cdot d}{k_e}\right) \right) ^2 } För cirkulärt fullgående ledningar


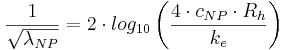\dfrac {1}{\sqrt {\lambda_{NP}}} = 2 \cdot log_{10} \left( \dfrac {4 \cdot c_{NP} \cdot R_h}{k_e} \right) Allmän formel


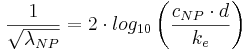\dfrac {1}{\sqrt {\lambda_{NP}}} = 2 \cdot log_{10} \left( \dfrac {c_{NP} \cdot d}{k_e}\right) För cirkulärt fullgående ledningar

där

λNP = Friktionstal (-)

cNP = Empirisk konstant (3,71)

Rh = Hydraulisk radie (m)

ke = Ekvivalent sandråhet (m)

d = Innerdiameter (m)


Se även

Hämtad från "https://sv.rilpedia.org/wiki/Nikuradse-Prandtls_formel"
Personliga verktyg