Darcy-Weisbachs ekvation

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Darcy-Weisbachs ekvation är en generell ekvation för beräkning av strömningsförluster och flöden vid framförallt stationar rörströmning i raka rör. Ekvationen är uppkallad efter Henry Darcy och Julius Weisbach.

Genom att anpassa friktionstalet (λ) för olika strömningsförhållanden i Moody-diagrammet, får Darcy-Weisbachs ekvation ett mycket brett tillämpningsområde inom rörströmningen. Darcy-Weisbachs ekvation brukar dels skrivas i en allmän form, dels i en form anpassad för cirkulärt fullgående ledningar.


Innehåll

Vid beräkning av höjdförlust

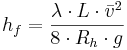h_f = \dfrac {\lambda \cdot L \cdot \bar v^2}{8 \cdot R_h \cdot g} Allmän form


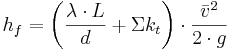h_f = \left( \dfrac {\lambda \cdot L } {d} + \Sigma k_t \right) \cdot \dfrac {\bar v^2}{2 \cdot g} För cirkullärt fullgående ledningar


där

hf = Strömningsförlust (mVp)

λ = Friktionstal (-)

L = Sektionens eller rörets längd (m)

d = Rörets innerdiameter (m)

Kt = Motståndskoefficient (-)

Fil:Del.gif = Medelhastighet (m/s)

Rh = Hydraulisk radie (m)

g = Tyngdacceleration (9,82 m/s2)


Vid beräkning av flödeshastigheter

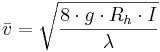\bar v = \sqrt {\dfrac {8 \cdot g \cdot R_h \cdot I}{\lambda}} Allmän formel


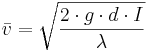\bar v = \sqrt {\dfrac {2 \cdot g \cdot d \cdot I}{\lambda}} För cirulärt fullgående ledningar

där

Fil:Del.gif = Medelhastighet (m/s)

g = Tyngdacceleration (9,82 m/s2)

Rh = Hydraulisk radie (m)

I = Fall (-)

λ = Friktionstal (-)

d = Rörets innerdiameter (m)


Vid flödesberäkning

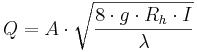Q = A \cdot \sqrt {\dfrac {8 \cdot g \cdot R_h \cdot I}{\lambda}} Allmän form


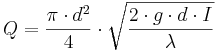Q = \dfrac {\pi \cdot d^2}{4} \cdot \sqrt {\dfrac {2 \cdot g \cdot d \cdot I}{\lambda}} För cirulärt fullgående ledningar

där

Q = Flöde (m3/s)

A = Våt tvärsnittsarea (m2)

Fil:Del.gif = Medelhastighet (m/s)

g = Tyngdacceleration (9,82 m/s2)

Rh = Hydraulisk radie (m)

I = Fall (-)

λ = Friktionstal (-)

π = Matematisk konstant (3.14159...)

d = Rörets innerdiameter (m)


Se även

Hämtad från "https://sv.rilpedia.org/wiki/Darcy-Weisbachs_ekvation"
Personliga verktyg
På andra språk