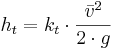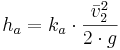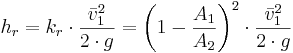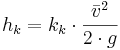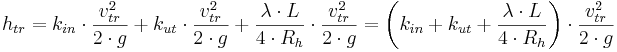Tilläggsförlust

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Tilläggsförluster (ht) eller lokala förluster kallas de punktmässiga strömningsförlusterna inom rörströmningen, som särskilt uppstår vid förekommande sektionsminskningar, sektionsökningar, rörböjar och brotrummepassager. Dessa tilläggsförluster måste adderas till de strömningsförluster som normalt uppstår vid stationär strömning i raka rör.

htotal = Σhf + Σht

där

htotal = Total energiförlust (mVp)

hf = Strömningsförlust (mVp)

ht = Tilläggsförlust (mVp)


Innehåll

Allmän formel

Den allmänna formeln för beräkning av enskilda tilläggsförluster brukar se ut enligt följande:

h_t = k_t \cdot \dfrac {\bar v^2}{2\cdot g}

där

kt = Motståndskoeficient (-)

Fil:Del.gif = Fluidens medelhastighet (m/s)

g = Tyngdaccelerationen (m/s2)


Motståndskoefficienten kt anger alltså engergiförlusten som en andel av hastighetshöjden. Värdet är en funktion av Reynolds tal och geometrin där förlusterna uppstår. Ibland brukar indexet t bytas ut mot indexet a (acceleration) när det rör sig om en hastighetsökning (sektionsminskning) och indexet r (retardation) när det rör sig om en hastighetssänkning (sektionsökning).


Sektionsminskning

h_a = k_a \cdot \dfrac {\bar v_2^2}{2\cdot g}

där 0,05 < ka < 0,60. Avrundade sektionsminskningar ger betydligt lägre värden på ka än skarpkantade sektionsminskningar. Högst värden fås när inloppsröret sticker ut.


Sektionsökning

h_r = k_r \cdot \dfrac {\bar v_1^2}{2\cdot g} = \left( 1 - \dfrac {A_1}{A_2} \right) ^2 \cdot \frac {\bar v_1^2}{2\cdot g}

där

A = Tvärsnittsarea (m2)

Om A1 << A2, till exempel om ledningen mynnar ut i en stor bassäng, brukar kr sättas till 1.


Rörkrökspassager

h_k = k_k \cdot \dfrac {\bar v^2}{2\cdot g}

där

0,05 < kk <0,50

Koefficienten kk är en funktion av avlänkningsvinkeln (θ), kvoten mellan rörkrökningsradien och ledningsdiametern (rk/d) samt den relativa skrovligheten (ke/d).


Brotrummepassager

htr = hf,in + hf,ut + hf,ror


h_{tr} = k_{in} \cdot \dfrac {v_{tr}^2}{2 \cdot g} + k_{ut} \cdot \dfrac {v_{tr}^2}{2 \cdot g} + \dfrac {\lambda \cdot L}{4 \cdot R_h} \cdot \dfrac {v_{tr}^2}{2 \cdot g} = \left(k_{in} + k_{ut} + \dfrac {\lambda \cdot L}{4 \cdot R_h} \right) \cdot \dfrac {v_{tr}^2}{2 \cdot g}

där

λ = Friktionstal (-)

L = Brotrummans längd (m)

Rh = Hydraulisk radie (m)


Vid skarpkantad inströmning sätts ofta kin = 0,50. Ofta sätts kut till 1,00. Om brotrummans längd (L) är kort (max 10-15 meter), utgörs nästan hela höjfdörlusten utav inloppets och utloppets beskaffenhet. Om brotrumman däremot är lång (100-200 meter eller mer) styrs höjdförlusten nästan enbart av brotrummans strömningsegenskaper. Notera att ovanstående ekvation gäller i princip bara för fullgående trummor.

Hämtad från "https://sv.rilpedia.org/wiki/Till%C3%A4ggsf%C3%B6rlust"
Personliga verktyg