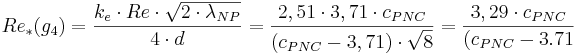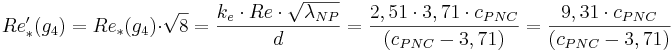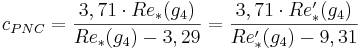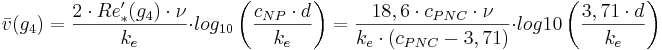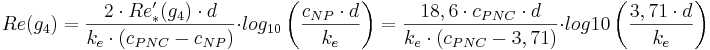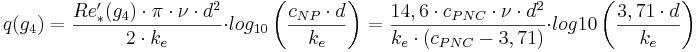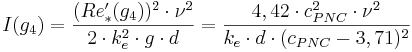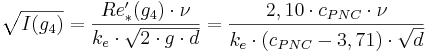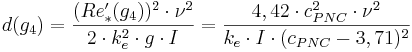Kritiskt värde (hydraulik)

Från Rilpedia

Texten från svenska Wikipedia

Det finns ett antal kritiska värden inom rörströmningen, som avgör vilka ekvationer som är tillämpliga när friktionstalet skall bestämmas.

Inom rörströmningen finns det fem olika strömningsgränser att ta hänsyn till. Dessa är

Gräns 1 (g₁) mellan Strömningstillstånd 1 och Övergångszon I.
Gräns 2 (g₂) mellan Övergångszon I och Strömningstillstånd 2A.
Gräns 3 (g₃) mellan Strömningstillstånd 2A och Övergångszon II.
Gräns 3` (g´₃) mellan Strömningstillstånd 2A och Strömningstillstånd 2B.
Gräns 4 (g₄) mellan Övergångszon II och Strömningstillstånd 2B.

Innehåll

1 Gräns 1
2 Gräns 2
3 Gräns 3
- 3.1 Hjälpekvationer för gräns 3
4 Gräns 3´
- 4.1 Hjälpekvationer för gräns 3´
5 Gräns 4
- 5.1 Några generella samband
- 5.2 Hjälpekvationer för gräns 4
6 Se även

Gräns 1

Denna gräns avgörs av storleken på det undre kritiska värdet på Reynolds tal (Re_k,u). När Re < Re_k,u får vi Strömningstillstånd 1 och Hagen-Poiseuilles lag kan användas. När Re > Re_k,u får vi Övergångszon I, där alla teoretiska flödesberäkningar blir mycket vanskliga.

För praktiskt bruk kan det undre kritiska värdet på Reynolds tal (Re_kt,u) sättas till ca 2000.

Gräns 2

Denna gräns avgörs av storleken på det övre kritiska värdet på Reynolds tal (Re_k,ö). När Re > Re_k,ö får vi Strömningstillstånd 2A, där Prandtl-Nikuradses formel bör användas. När Re > Re_k,ö får vi Övergångszon I, där alla teoretiska flödesberäkningar blir mycket vanskliga.

För praktiskt bruk kan det övre kritiska värdet på Reynolds tal (Re_k,ö) sättas till ca 4000.

Gräns 3

Denna gräns avgörs av storleken på skrovlighetens reynoldstal (Re_*). När Re_* < 3,1-4 får vi Strömningstillstånd 2A, där Prandtl-Nikuradses formel bör användas. När Re_* > 3,1-4 får vi övergångszon II, där Prandtl-Nikuradse-Colebrooks formel bör användas.

Hjälpekvationer för gräns 3

För att underlätta bedömningen av vilken ekvation som är tillämplig, kan det kritiska fallet (I(g₃)) och den kritiska innerdiametern d(g₃)) beräknas enligt följande:

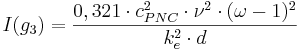$I(g_{3}) = \frac {0,321 \cdot c_{PNC}^2 \cdot \nu^2 \cdot (\omega -1)^2}{k_e^2 \cdot d}$ Kritiskt fall

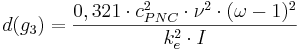$d(g_{3}) = \frac {0,321 \cdot c_{PNC}^2 \cdot \nu^2 \cdot (\omega -1)^2}{k_e^2 \cdot I}$ Kritisk diameter

där

I(g₃) = Kritiskt fall vid gräns 3 (-)

c_PNC = Numerisk konstant i Prandtl-Nikuradse-Colebrooks formel (-)

ν = Kinematisk viskositet (m²/s)

ω = Empiriskt vågighetstal (-)

k_e = Ekvivalent sandråhet (m)

d = Innerdiameter (m)

d(g₃) = Kritisk innerdiameter vid gräns 3 (m)

I = Fall (-)

Notera att dessa hjälpekvationer bara gäller när det empiriska vågighetstalet överstiger 1. Annars saknas reella värden på det kritiska fallet och den kritiska innerdiametern. Reynolds tal (Re)måste också överstiga den övre kritiska värdet för Reynolds tal (Re_k,ö).

Gräns 3´

När den relativa skrovligheten (ε) understiger 0,001, brukar man beräkningsmässigt ofta strunta i övergångszon II. Således får vi en direktövergång mellan Strömningstillstånd 2A och Strömningstillstånd 2B. För Strömningstillstånd 2A gäller Prandtl-Nikuradses formel och för strömningszon 2B gäller Nikuradse-Prandtls formel.

Hjälpekvationer för gräns 3´

För att underlätta bedömningen av vilken ekvation som är tillämplig, kan man även beräkna kritiskt fall (I(g´₃)) och kritisk innerdiameter d(g´₃)) enligt följande:

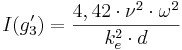$I(g'_{3}) = \frac {4,42 \cdot \nu^2 \cdot \omega^2}{k_e^2 \cdot d}$ Kritiskt fall

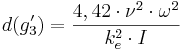$d(g'_{3}) = \frac {4,42 \cdot \nu^2 \cdot \omega^2}{k_e^2 \cdot I}$ Kritisk diameter

där

I(g´₃) = Kritiskt fall vid gräns 3´ (-)

ν = Kinematisk viskositet (m²/s)

ω = Empiriskt vågighetstal (-)

k_e = Ekvivalent sandråhet (m)

d = Innerdiameter (m)

d(g´₃) = Kritisk innerdiameter vid gräns 3´ (m)

I = Fall (-)

Notera att dessa hjälpekvationer bara är lämpliga när den relativa skrovligheten (ε) understigen 0,001. Annars är det gräns 3 och gräns 4 som gäller.

Gräns 4

Denna gräns avgörs av storleken på skrovlighetens reynoldstal (Re_*). När Re_* > 45,4-58,8 får vi Strömningstillstånd 2B, där Nikuradse-Prandtls formel är tillämplig. När Re_* < 45,4-58,8 får vi övergångszon II, där Prandtl-Nikuradse-Colebrooks formel bör användas.

Några generella samband

Generellt gäller sambanden:

$Re_*(g_4) = \dfrac {k_e \cdot Re \cdot \sqrt {2 \cdot \lambda_{NP}}}{4 \cdot d} = \dfrac {2,51 \cdot 3,71 \cdot c_{PNC}}{(c_{PNC} - 3,71) \cdot \sqrt {8}} = \dfrac {3,29 \cdot c_{PNC}}{(c_{PNC} - 3.71}$

$Re'_*(g_4) = Re_*(g_4) \cdot \sqrt {8} = \dfrac {k_e \cdot Re \cdot \sqrt {\lambda_{NP}}}{d} = \dfrac {2,51 \cdot 3,71 \cdot c_{PNC}}{(c_{PNC} -3,71)} = \dfrac {9,31 \cdot c_{PNC}}{(c_{PNC} -3,71)}$

$c_{PNC} = \dfrac {3,71 \cdot Re_*(g_4)}{Re_*(g_4) - 3,29} = \dfrac {3,71 \cdot Re'_*(g_4)}{Re'_*(g_4) - 9,31}$

där

Re_*(g₄) = Skrovlighetens reynoldstal vid gräns 4 (-)

k_e = Ekvivalent sandråhet (-)

Re = Reynolds tal (-)

λ_NP = Friktionstal enligt Nikuradse-Prandtls formel (-)

d = Innerdiameter (-)

c_PNC = Empirisk konstant i Prandtl-Nikuradse-Colebrooks formel (-)

Re´_*(g₄) = Specialuttryck av skrovlighetens reynoldstal vid gräns 4 (-)

Hjälpekvationer för gräns 4

Då gräns 4 är aktuell för många hydrotekniska tillämpningar inom rörströmningen, finns det gott om matematiskt definierade gränsvärden.

Kritisk medelhastighet

$\bar v(g_4) = \dfrac {2 \cdot Re'_*(g_4) \cdot \nu}{k_e} \cdot log_{10} \left( \dfrac {c_{NP} \cdot d}{k_e} \right) = \dfrac {18,6 \cdot c_{PNC} \cdot \nu}{k_e \cdot (c_{PNC} -3,71)} \cdot log{10} \left( \dfrac {3,71 \cdot d}{k_e} \right)$

där

Fil:Del.gif(g₄) = Kritisk medelhastighet vid gräns 4 (m/s)

Re´_*(g₄) = Specialuttryck av skrovlighetens reynoldstal vid gräns 4 (-)

ν = Kinematisk viskositet (m²/s)

k_e = Ekvivalent sandråhet (m)

c_NP = Empirisk konstant i Nikuradse-Prandtls formel (3,71)

d = Innerdiameter (m)

c_PNC = Empirisk konstant i Prandtl-Nikuradse-Colebrooks formel (-)

Kritiskt reynoldstal

$Re(g_4) = \dfrac {2 \cdot Re'_*(g_4) \cdot d}{k_e \cdot (c_{PNC} - c_{NP})} \cdot log_{10} \left( \dfrac {c_{NP} \cdot d}{k_e} \right) = \dfrac {18,6 \cdot c_{PNC} \cdot d}{k_e \cdot (c_{PNC} - 3,71)} \cdot log{10} \left( \dfrac {3,71 \cdot d}{k_e} \right)$

där

Re(g₄) = Kritisk reynoldstal vid gräns 4 (-)

Re´_*(g₄) = Specialuttryck av skrovlighetens reynoldstal vid gräns 4 (-)

d = Innerdiameter (m)

k_e = Ekvivalent sandråhet (m)

c_NP = Empirisk konstant i Nikuradse-Prandtls formel (3,71)

c_PNC = Empirisk konstant i Prandtl-Nikuradse-Colebrooks formel (-)

Kritiskt flöde

$q(g_4) = \dfrac {Re'_*(g_4) \cdot \pi \cdot \nu \cdot d^2}{2\cdot k_e} \cdot log_{10} \left( \dfrac {c_{NP} \cdot d}{k_e} \right) = \dfrac {14,6 \cdot c_{PNC} \cdot \nu \cdot d^2}{k_e \cdot (c_{PNC} - 3,71)} \cdot log{10} \left( \dfrac {3,71 \cdot d}{k_e} \right)$

där

q(g₄) = Kritiskt flöde vid gräns 4 (m³/s)

Re´_*(g₄) = Specialuttryck av skrovlighetens reynoldstal vid gräns 4 (-)

π = Matematisk konstant (3,14159...)

ν = Kinematisk viskositet (m²/s)

d = Innerdiameter (m)

k_e = Ekvivalent sandråhet (m)

c_NP = Empirisk konstant i Nikuradse-Prandtls formel (3,71)

c_PNC = Empirisk konstant i Prandtl-Nikuradse-Colebrooks formel (-)

Kritiskt fall

$I(g_4) = \dfrac {(Re'_*(g_4))^2 \cdot \nu^2}{2 \cdot k_e^2 \cdot g \cdot d} = \dfrac {4,42 \cdot c_{PNC}^2 \cdot \nu^2}{k_e \cdot d \cdot (c_{PNC} - 3,71)^2}$

och

$\sqrt {I(g_4)} = \dfrac {Re'_*(g_4) \cdot \nu}{k_e \cdot \sqrt {2 \cdot g \cdot d}} = \dfrac {2,10 \cdot c_{PNC} \cdot \nu}{k_e \cdot (c_{PNC} - 3,71)\cdot \sqrt {d}}$

där

I(g₄) = Kritiskt fall vid gräns 4 (-)

Re´_*(g₄) = Specialuttryck av skrovlighetens reynoldstal vid gräns 4 (-)

ν = Kinematisk viskositet (m²/s)

k_e = Ekvivalent sandråhet (m)

g = Tyngdacceleration (m/s²)

d = Innerdiameter (m)

c_PNC = Empirisk konstant i Prandtl-Nikuradse-Colebrooks formel (-)

Kritisk ekvivalent sandråhet

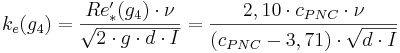
$k_e(g_4) = \dfrac {Re'_*(g_4) \cdot \nu}{\sqrt {2 \cdot g \cdot d \cdot I}} = \dfrac {2,10 \cdot c_{PNC} \cdot \nu}{(c_{PNC} - 3,71)\cdot \sqrt {d \cdot I}}$

där

k_e(g₄) = Kritisk ekvivalent sandråhet vid gräns 4 (-)

Re´_*(g₄) = Specialuttryck av skrovlighetens reynoldstal vid gräns 4 (-)

ν = Kinematisk viskositet (m²/s)

g = Tyngdacceleration (m/s²)

d = Innerdiameter (m)

I = Fall (-)

c_PNC = Empirisk konstant i Prandtl-Nikuradse-Colebrooks formel (-)

Kririsk innerdiameter

$d(g_4) = \dfrac {(Re'_*(g_4))^2 \cdot \nu^2}{2 \cdot k_e^2 \cdot g \cdot I} = \dfrac {4,42 \cdot c_{PNC}^2 \cdot \nu^2}{k_e \cdot I \cdot (c_{PNC} - 3,71)^2}$

där

d(g₄) = Kritisk innerdiameter vid gräns 4 (m)

Re´_*(g₄) = Specialuttryck av skrovlighetens reynoldstal vid gräns 4 (-)

ν = Kinematisk viskositet (m²/s)

k_e = Ekvivalent sandråhet (m)

g = Tyngdacceleration (m/s²)

I = Fall (-)

c_PNC = Empirisk konstant i Prandtl-Nikuradse-Colebrooks formel (-)

Se även

Rörströmning

Kritiskt värde (hydraulik)

Från Rilpedia

Innehåll

Gräns 1

Gräns 2

Gräns 3

Hjälpekvationer för gräns 3

Gräns 3´

Hjälpekvationer för gräns 3´

Gräns 4

Några generella samband

Hjälpekvationer för gräns 4

Kritisk medelhastighet

Kritiskt reynoldstal

Kritiskt flöde

Kritiskt fall

Kritisk ekvivalent sandråhet

Kririsk innerdiameter

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda