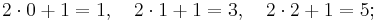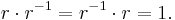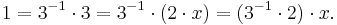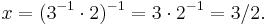Ekvation
Från Rilpedia
| Matematiska begrepp |
|---|
Inom matematiken är en ekvation ett sätt att med symboler beskriva att två matematiska objekt är lika. (Ordet ekvation betyder på latin "likhet".)
Den matematik som studeras inom grundskolan behandlar ekvationer där de matematiska objekten är tal. Exempelvis lär man sig där att 2 + 3 = 5. Denna ekvation visar två representationer av talet fem: Dels som symbolen 5, dels som summan av talen två och tre. Med en ekvation kan man beskriva ett och samma objekt på två olika sätt.
Den matematik som studeras inom gymnasieskolan behandlar ekvationer där objekten är tal och funktioner. Exempelvis lär man sig inom trigonometri den så kallade Trigonometriska ettan:
- sin2v + cos2v = 1.
Detta är ett samband mellan de trigonometriska funktionerna sinus (sin) och cosinus (cos) och den gäller för varje val av vinkeln v.
Den matematik som studeras inom högskolan behandlar ekvationer där objekten är tal, funktioner och mängder. Exempelvis lär man sig att mängden av rationella tal är lika med mängden av alla tal som kan skrivas som periodiska decimalutvecklingar.
Att lösa en ekvation
Då man talar om att lösa ekvationen 2x + 1 = 4, menar man att man finner alla tänkbara tal x som gör det möjligt att skriva talet fyra på formen 2x + 1. Då man försöker att lösa en ekvation är det viktigt att specificera lösningsmängden, det vill säga den mängd av tal inom vilken man får lov att söka lösningen.
Om man skall söka bland de naturliga talen 0, 1, 2, 3, ..., så finner man inte någon lösning. Det enklaste sättet att verifiera detta, är att pröva de olika talen 0, 1, 2,..., i tur och ordning och se om något av dem uppfyller ekvationen 2x + 1 = 4. Man behöver inte pröva varje tal i denna uppräkneliga mängd, eftersom
Ersätter man symbolen x med naturliga tal större än talet 2, blir talet 2x + 1 större än talet 5.
Om man däremot skall söka i den större mängden Q, bestående av de rationella talen, så finner man en lösning. Den kan bestämmas på följande sätt.
Talet fyra kan skrivas som:
- 4 = 3 + 1.
Detta innebär att vi har två sätt att skriva talet fyra: Dels som summan 3 + 1 och dels som summan 2x + 1. Talet 1 finns med i båda dessa uttryck. Detta innebär att talen 3 och 2x är lika, det vill säga vi har fått en ny ekvation:
- 3 = 2x.
Varje rationellt tal, r, har en unik multiplikativ invers; ett associerat rationellt tal betecknat r − 1 sådant att:
Den multiplikativa inversen till det rationella talet 3 är det rationella talet 3 − 1 = 1 / 3. Om vi multiplicerar ekvationen 3 = 2x med talet 3 − 1, får vi följande ekvation:
Detta visar att det rationella talet x är en multiplikativ invers till det rationella talet 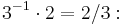
Eftersom varje rationellt tal endast har en multiplikativ invers, är x = 3 / 2 den enda lösningen till ekvationen 2x = 3, och därmed även till ekvationen 2x + 1 = 4.
Mer kortfattat kan man skriva ovanstående resonemang på följande sätt:
Allmänt så kan en ekvation ha ingen, en eller flera lösningar. Ovanstående enkla ekvation har exakt en lösning.
Se även