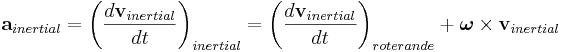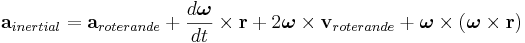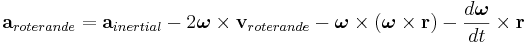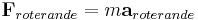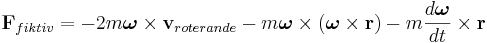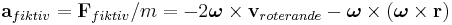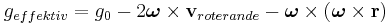Corioliseffekten

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Ett lågtryck över Island som på grund av corioliskraften roterar moturs.
Centrum av ett lågtrycksområde på norra halvklotet. Tryckgradientens riktning anges med blå pilar. Corioliskraften, alltid vinkelrät mot luftmassans hastighetsriktning, visas med röda pilar.

Corioliskraften är en fiktiv kraft som verkar på massor i roterande system.

Corioliskraften är uppkallad efter Gaspard Gustave Coriolis (1792-1843) som 1835 skrev en uppsats om denna kraft. Coriolis var intresserad av att förbättra franskbyggda maskiner, i synnerhet sådana med roterande delar. Dessa påverkas av en centrifugaleffekt som, om inte materialet är starkt nog, kan spränga konstruktionen. Coriolis var intresserad av hur centrifugaleffekten påverkades om vissa delar i maskinen också rörde sig relativt rotationen. Han fann då att den vanliga centrifugaleffekten ändrades något i storlek och riktning.

Till skillnad från till exempel den elektromagnetiska kraften är corioliskraften ingen egentlig kraft utan en fiktiv kraft.

Inom psykologin menas med Corioliseffekt (även känd som Coriolis illusion) de problem med rörelsesjuka och desorientering som kan drabba astronauter och flygplanspiloter på grund av Corioliskraften.

Innehåll

Corioliskrafter orsakade av jordens rotation

Vi tänker oss ett föremål på norra halvklotet som till en början rör sig i nord-sydlig riktning utan att påverkas av andra krafter än tyngdkraften. Relativt den roterande jordytan uppkommer då en skenbar acceleration på grund av att avståndet till jordens rotationsaxel ökar. Denna skenbara acceleration kan anses svara mot en fiktiv kraft riktad åt väster och denna kraft är just Corioliskraften. En observatör som rör sig med jordytan kan beräkna den resulterande kraft (summan av alla krafter) som verkar på föremålet genom att behandla Corioliskraften som en verklig kraft. Corioliskraften är vinkelrät både mot objektets rörelseriktning och jordens rotationsaxel.

Jordens rotation kan således orsaka Corioliskrafter och dessa har en stor inverkan på klimatet. Corioliskraften påverkar stora luftmassor och kan få stormar och orkaner att rotera. Den ger också upphov till så kallade uppvällningar vilka ligger till grund för den höga halten av biomassa i hav utmed västkuster.

Corioliseffekten har ett avgörande inflytande på strömningarna i atmosfären och i haven då den söker hindra all horisontell rörelse genom dess tendens att överföra denna till en cirkelrörelse. Det krävs därför stora krafter med ursprung i horisontella tryckskillnader för att få varm luft från de upphettade tropikerna att tränga norrut och avkylas och kall luft från polerna att komma söderut och värmas upp.

Jämfört med gravitationskraften är Corioliskraften en mycket svag kraft. Den måste verka under lång tid och över stora avstånd för att ge tydliga effekter.

Myter

Många av de förklaringar till corioliseffekten som ges i form av rullande bollar på karusellgolv, flygplan som flyger söderut eller luftpaket som rör sig från ekvatorn till 30 graders latitud är antingen felaktiga eller vilseledande.

En vanligt förekommande myt (så vanlig att den brukar läras ut i klassrum) är att Corioliskraften får utrinnande vatten i badkar och handfat att rotera, och att det då skulle rotera åt olika håll på norra och södra halvklotet. Även om det stämmer i princip, är corioliskraften alldeles för svag för att ha någon påverkan på så små system. Det är slumpen och främst kärlets form som avgör vattnets rotationsriktning.

Enligt en gammal sägen tillfångatogs en tysk ubåtskapten av de allierade under första världskriget och låstes in i en fönsterlös hytt. Han skulle sedan med handfatets hjälp ha avgjort när båten passerade ekvatorn genom att studera vattenvirveln när han tömde handfatet. För att corioliskraften ska kunna få en påvisbar effekt i ett handfat måste handfatet ha en diameter på 10-tals meter samt ha ett litet hål i mitten.

Härledning

Förhållandet mellan en acceleration i ett inertialsystem och motsvarande acceleration i ett roterande koordinatsystem som roterar enligt rotationshastighetsvektorn 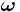\boldsymbol\omega kan skrivas

\mathbf{a}_{inertial}= \left(\frac{d\mathbf{v}_{inertial}}{dt}\right)_{inertial} =\left(\frac{d\mathbf{v}_{inertial}}{dt}\right)_{{roterande}} + \boldsymbol\omega \times \mathbf{v}_{inertial}

där vi har utnyttjat relationen för tidsderivatan för en vektor i roterande koordinater. Uttrycket

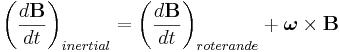\left(\frac{d\mathbf{B}}{dt}\right)_{inertial} = \left(\frac{d\mathbf{B}}{dt}\right)_{{roterande}} + \boldsymbol\omega \times \mathbf{B},

gäller för en godtycklig vektor 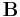\mathbf{B}. Då

\mathbf{v}_{inertial} = \mathbf{v}_{{roterande}}+ \boldsymbol\omega \times \mathbf{r}\ ,

blir accelerationen

\mathbf{a}_{inertial} = \left(\frac{d ( \mathbf{v}_{{roterande}} + \boldsymbol\omega \times \mathbf{r})}{dt} \right)_{{roterande}} + \boldsymbol\omega \times \mathbf{v}_{{roterande}} + \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf{r} )

eller, ekvivalent,

\mathbf{a}_{inertial} = \mathbf{a}_{{roterande}} + \frac{d \boldsymbol\omega}{dt} \times \mathbf{r} + 2 \boldsymbol\omega \times \mathbf{v}_{{roterande}} + \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf{r} )

Accelerationen i den roterande referensramen är

\mathbf{a}_{{roterande}} = \mathbf{a}_{inertial} - 2 \boldsymbol\omega \times \mathbf{v}_{roterande} - \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf{r} ) - \frac{d \boldsymbol\omega}{dt} \times \mathbf{r}

Då kraften i den roterande referensramen är

\mathbf{F}_{{roterande}} = m \mathbf{a}_{{roterande}}\

och, enligt definition,

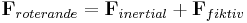\mathbf{F}_{{roterande}} = \mathbf{F}_{inertial} + \mathbf{F}_{{fiktiv}}\ ,

blir den fiktiva kraften

\mathbf{F}_{{fiktiv}} = - 2 m \boldsymbol\omega \times \mathbf{v}_{{roterande}} - m \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf{r} ) - m \frac{d \boldsymbol\omega }{dt} \times \mathbf{r}

där den första termen är Corioliskraften, den andra termen är centrifugalkraften och den tredje är Eulerkraften.

Centrifugalacceleration och Coriolisacceleration

Tyngdkraftspåverkan

Tyngdkraften är summan av de krafter som verkar på en kropp på grund av gravitationen och jordens rotation. Om vi utgår från

\mathbf{a}_{{fiktiv}} = \mathbf{F}_{fiktiv}/{m} = - 2\boldsymbol\omega \times \mathbf{v}_{{roterande}} - \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf{r} )

(för jordens rotation är Eulerkraften = 0), kan vi skriva den effektiva tyngdkraften som

{g}_{effektiv} = {g}_{0} - 2\boldsymbol\omega \times \mathbf{v}_{{roterande}} - \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf{r} )

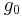där {g}_{0}\ är gravitationskraftens värde mätt av en stillastående (icke-roterande) observatör.

Centrifugalaccelerationen 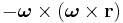- \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf{r}) är låg jämfört med tyngdaccelerationen. Den når sitt största värde vid ekvatorn där den är cirka 0.3 % av tyngdaccelerationen.

Vi ser av den andra termen i högerledet att Corioliskraften ger ett positivt eller negativt tillskott beroende på riktningen av 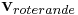\mathbf{v}_{{roterande}}.

Se även

Källor

  • Thomas Brandt (2003). Vertigo: Its Multisensory Syndromes. Springer, p. 416. ISBN 0387405003.
  • Fred H. Previc, William R. Ercoline (2004). Spatial Disorientation in Aviation. Reston, VA: American Institute of Aeronautics and Astronautics, Inc, p. 249. ISBN 1563476541.


Externa länkar

Hämtad från "https://sv.rilpedia.org/wiki/Corioliseffekten"
Personliga verktyg