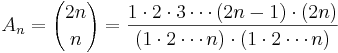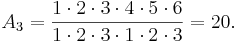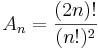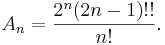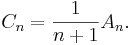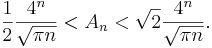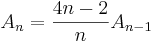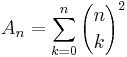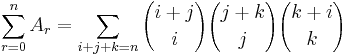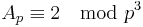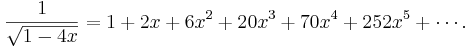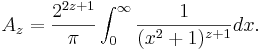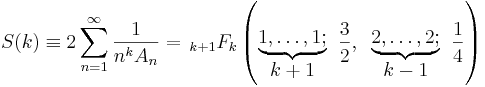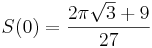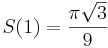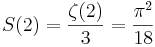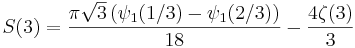Central binomialkoefficient

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
1
1   1
1   2   1
1   3   3   1
1   4   6   4   1
1   5  10  10   5   1
1   6  15  20  15   6   1
Centrala binomialkoefficienter i Pascals triangel.

En central binomialkoefficient är inom matematik ett tal på formen

A_n = {2n \choose n} = \frac{1 \cdot 2 \cdot 3 \cdots (2n-1) \cdot (2n)}{(1 \cdot 2 \cdots n) \cdot (1 \cdot 2 \cdots n)}

där n är ett heltal och 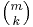\begin{matrix} {m \choose k} \end{matrix} betecknar en binomialkoefficient. Exempelvis är

A_3 = \frac{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6}{1 \cdot 2 \cdot 3 \cdot 1 \cdot 2 \cdot 3} = 20.

Heltalsföljden av centrala binomialkoefficienter för n = 0, 1, 2, ... börjar 1, 2, 6, 20, 70, 252, 924, 3432, 12870, 48620, ... (talföljd A000984 i OEIS). De centrala binomialkoefficienterna utgör den centrala kolumnen i Pascals triangel.

Innehåll

Alternativa representationer

En central binomialkoefficient kan skrivas med fakulteter som

A_n = \frac{(2n)!}{(n!)^2}

och med en semifakultet som

A_n = \frac{2^n(2n-1)!!}{n!}.

De centrala binomialkoefficienterna är intimt förbundna med catalantalen Cn som ges av

C_n = \frac{1}{n+1} A_n.

Storleksuppskattning

Enligt Stirlings formel gäller

\frac{1}{2} \frac{4^n}{\sqrt{\pi n}} < A_n < \sqrt{2} \frac{4^n}{\sqrt{\pi n}}.

Samband mellan binomialkoefficienter

Ett stort antal samband mellan centrala binomialkoefficienter samt mellan centrala binomialkoefficienter och andra binomialkoefficienter kan härledas. Några exempel är:

A_n = \frac{4n-2}{n} A_{n-1}
A_n = \sum_{k=0}^n {n \choose k}^2
\sum_{r=0}^n A_r = \sum_{i+j+k=n} {i+j\choose i} {j+k\choose j} {k+i \choose k}

Listan (Hubbard & Roby) innehåller fler formler av samma typ.

Talteoretiska egenskaper

Paul Erdős och Ronald Graham formulerade 1980 en förmodan att den centrala binomialkoefficienten An aldrig är kvadratfri för n > 4. Ett fullständigt bevis gavs 1996 av A. Granville och O. Ramare.

Wolstenholmes sats kan användas för att visa att

A_p \equiv2\mod p^3

för alla primtal p > 3.

Genererande funktion

De centrala binomialkoefficienterna har den genererande funktionen

\frac{1}{\sqrt{1-4x}} = 1 + 2x + 6x^2 + 20x^3 + 70x^4 + 252x^5 + \cdots.

Generalisering till komplexa tal

Gammafunktionen kan användas för att utvidga definitionen till komplexa tal z enligt

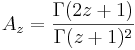A_z = \frac{\Gamma(2z+1)}{\Gamma(z+1)^2}.

De centrala binomialkoefficienterna ges även av integralen

A_z = \frac{2^{2z+1}}{\pi} \int_0^\infty \frac{1}{(x^2+1)^{z+1}} dx.

Serier av inversa centrala binomialkoefficienter

I allmänhet är

S(k) \equiv 2 \sum_{n=1}^\infty \frac{1}{n^k A_n} = {\,_{k+1}F_k} \left( \begin{matrix} \\ \underbrace{ 1, \ldots, 1; } \\ k+1 \end{matrix} \;\; \frac{3}{2},\;\; \begin{matrix} \\ \underbrace{ 2, \ldots, 2; } \\ k-1 \end{matrix} \;\; \frac{1}{4} \right)

där pFq betecknar en hypergeometrisk funktion. Som specialfall gäller exempelvis

S(0) = \frac{2\pi\sqrt 3 + 9}{27}
S(1) = \frac{\pi\sqrt 3}{9}
S(2) = \frac{\zeta(2)}{3} = \frac{\pi^2}{18}
S(3) = \frac{\pi \sqrt 3 \left( \psi_1(1/3)-\psi_1(2/3) \right)}{18} - \frac{4 \zeta(3)}{3}

där ζ betecknar Riemanns zeta-funktion och ψn betecknar en polygammafunktion. Fler sådana summor ges av Weisstein.

Källor

Hämtad från "https://sv.rilpedia.org/wiki/Central_binomialkoefficient"
Personliga verktyg
På andra språk