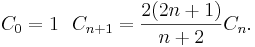Catalantal

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Catalantalen utgör talföljden

(C0, C1, C2, C3, C4,...) = (1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, ...)

som är uppkallade efter den belgiska matematikern Eugène Charles Catalan (1814–1894). Catalantalen har visats ange antalen för en mycket stor uppsättning olika kombinatoriskt intressanta familjer av mängder.

Egenskaper

Algebraiskt kan catalantalen definieras genom

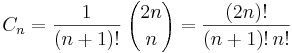C_n = \frac1{(n+1)!} \; {2n \choose n} = \frac{(2n)!}{(n+1)!\,n!} \, (där ! står för fakultetsfunktionen och 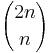{2n \choose n}\, är en binomialkoefficient).

Catalantalen kan också beskrivas rekursivt:

C_0 = 1 ~~ C_{n+1} = \sum_{i=0}^n C_iC_{n-i}

eller:

C_0 = 1 ~~ C_{n+1} = \frac{2(2n+1)}{n+2}C_n.

Tillämpningar

Cn är antalet monotona vägar genom ett n × n-rutnät av kvadrater som inte går ovanför diagonalen i rutnätet. En monoton väg är en väg som börjar i nedre vänstra hörnet och rör sig upp till övre hörna hörnet, genom att antingen röra sig uppåt eller åt höger.

Catalan number 4x4 grid example.svg

Cn är också antalet sätt en konvex polygon med n + 2 sidor kan delas in i trianglar genom att dra linjer mellan hörn.


Encoder Disc (3-Bit).svg Denna artikel om kombinatorik eller diskret matematik är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Catalantal"
Personliga verktyg