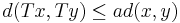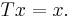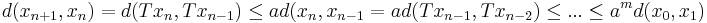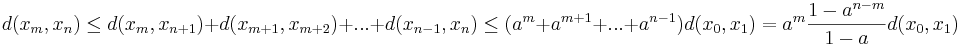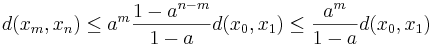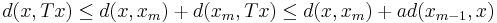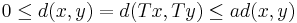Från Rilpedia

Banachs fixpunktssats, är en matematisk sats inom funktionalanalys som säger att en kontraktionsavbildning alltid har en unik fixpunkt. Satsen är uppkallad efter Stefan Banach som formulerade den 1922.^[1]

Innehåll 1 Banachs fixpunktssats 2 Bevis 3 Tillämpningar 4 Noter 5 Referenser

Banachs fixpunktssats

Om (X,d) är ett fullständigt metriskt rum med 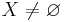och T en avbildning, 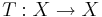. Om T är en kontraktionsavbildning, dvs det existerar ett positivt reellt tal a < 1 så att

för alla x och y i X. Då har T exakt en fixpunkt, dvs det existerar exakt ett x i X så att

Bevis

Välj ett godtyckligt 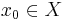och konstruera sedan följden (x_n) genom:

x₁ = Tx₀

x₂ = Tx₁ = T²x₀

x_n = Tx_{n − 1} = Tⁿx₀

Då T är en kontraktionsavbildning fås att:

För godtyckliga naturliga tal m och n med m < n får vi nu, genom triangelolikheten och att a < 1, att:

Här kan vänsterledet göras godtyckligt litet, eftersom d(x₀,x₁) är fixt och när 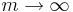. Detta ger att följden (x_n) är en Cauchyföljd och då X är fullständigt finns det ett gränsvärde x så att .

x är i själva verket fixpunkten för T, då

eftersom d(x,x_m) och d(x_{m − 1},x) kan göras godtyckligt litet för stora m (x_m går mot x ger att avståndet går mot noll).

Antag att det finns en annan fixpunkt för T kallad y, då vi får:

då a är mindre än 1 ger detta att d(x,y) = 0 och därmed att x = y.

Tillämpningar

Banachs fixpunktssats kan användas till att bevisa många andra satser, däribland inversa funktionssatsen och Picard-Lindelöfs sats om existensen till och unikheten hos lösningar till vissa ordinära differentialekvationer.

Noter

1. ↑ Stefan Banach, Sur les opérations dans les ensembles abstracts et leur application aux équations intégrales (1922) Fundamenta Mathematicae. 3. sid. 133-181. På internet 2009-03-21.

Referenser

• Kreyszig, Erwin: Introductory Functional Analysis with Applications, John Wiley & Sons, 1978. ISBN 0-471-50731-8. 
• Hille, Einar: Ordinary Differential Equations in the Complex Domain, Dover Publications, 1976. ISBN 0-486-69620-0.