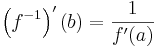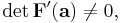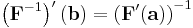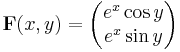Inversa funktionssatsen

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Inversa funktionssatsen är en matematisk sats inom differentialkalkyl. Satsen ger tillräckliga villkor för att en funktion ska vara inverterbar i en omgivning till en given punkt och en formel för beräkning av derivatan av den inversa funktionen.

Innehåll

Inversa funktionssatsen

Envariabelanalys

Om f är kontinuerligt deriverbar med nollskild derivata i punkten a så är f inverterbar i en omgivning till a. Om f(a) = b kan derivatan av f − 1 beräknas i punkten b genom:

\left(f^{-1}\right)'(b) = \frac{1}{f'(a)}

Flervariabelanalys

Låt 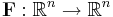\mathbf F:\R^n\to\R^n vara en kontinuerligt deriverbar avbildning. Om 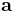\mathbf a är en punkt så att Jacobideterminanten är nollskilld i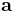 \mathbf a

\det \mathbf F'(\mathbf a) \neq 0,

så finns det omgivningar U och V kring 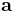\mathbf a respektive 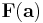\mathbf F(\mathbf a) så att avbildningen 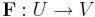\mathbf F: U \to V är bijektiv och inversen 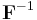\mathbf F^{-1} är kontinuerligt deriverbar.

Om 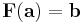\mathbf F(\mathbf a) = \mathbf b så kan Jacobimatrisen till 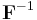\mathbf F^{-1} kan beräknas med

\left( \mathbf F^{-1} \right)' (\mathbf b) = \left( \mathbf F'(\mathbf a) \right)^{-1}

Bevis

Det finns många bevis för inversa funktionssatsen. Det enklaste bygger på satsen om största och minsta värde. Ett generellare bevis bygger på Banachs fixpunktssats, som även kan användas till att bevisa en generalisering av satsen som gäller i oändlighetsdimensionella vektorrum.

Exempel

Betrakta 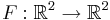F:\R^2 \to \R^2 definierad av

\mathbf F (x,y) = \begin{pmatrix} e^x \cos y \\ e^x \sin y \end{pmatrix}

Jacobimatrisen blir 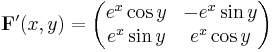\mathbf F'(x,y) = \begin{pmatrix} e^x \cos y & -e^x \sin y \\ e^x \sin y & e^x \cos y \end{pmatrix} så att determinaten är

\det \mathbf F'(x,y) = e^{2x} \cos^2 y + e^{2x} \sin^2 y = e^{2x}.

Då e2x är nollskild för alla reella x ger inversa funktionssatsen att varje \mathbf q \in \R^2 har en omgivning där funktionen är inverterbar.

Se även

Referenser

  • Forsling, Göran; Mats Neymark: Matematisk analys i en variabel, Liber, 2004, sid. 192. ISBN 91-47-05188-4. 
  • Persson, Arne; Lars-Christer Böiers: Analys i flera variabler, Studentlitteratur, 2005. ISBN 91-44-03869-0. 
Hämtad från "https://sv.rilpedia.org/wiki/Inversa_funktionssatsen"
Personliga verktyg