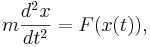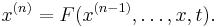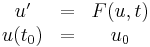Ordinär differentialekvation
Från Rilpedia
Inom matematik så är en ordinär differentialekvation (eller ODE) en ekvation som innehåller funktioner som endast beror på en oberoende variabel, och en eller flera av dess derivator med avseende på den variabeln.
Ett exempel i fysiken är Newtons andra rörelselag, som ger differentialekvationen
för rörelsen hos en partikel med massan m. I allmänhet beror kraften F på positionen av partikeln x, och alltså så finns den okända variabeln x på båda sidor av differentialekvationen.
Ordinära differentialekvationer bör särskiljas från partiella differentialekvationer där det finns partiella derivator med avseende på flera oberoende variabler.
Ordinära differentialekvationer förekommer i många olika sammanhang såsom geometri, mekanik och astronomi. Många berömda matematiker har studerat differentialekvationer och bidragit till forskningsfältet, såsom Newton, Leibniz, släktingarna Bernoulli, Riccati, Clairaut, d'Alembert och Euler.
Mycket arbete har lagts ner på problemet hur man löser ordinära differentialekvationer.
I fallet där ekvationen är linjär med konstanta koefficienter så kan den lösas med analytiska metoder (dvs med papper och penna). Tyvärr är många intressanta differentialekvationer icke-linära och kan i allmänhet inte lösas exakt. Genom datorberäkningar (numerisk analys) så kan man beräkna lösningarna approximativt, och ofta upp till godtyckligt hög noggrannhet.
Innehåll |
Formell definition
En allmän ODE har formen
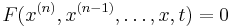 ,
,
för någon funktion F. Genom att låta x vara en vektorvärd funktion kan vi täcka in fallet när vi har system av differentialekvationer. Man kan låta x ta värden i allmänna Banachrum men vi kommer behandla fallet då x tar värden i 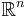 .
.
Det vanligaste i tillämpningar är att ekvationen är på normalform vilket innebär att den kan skrivas
En ekvation på normalform kan reduceras till en ekvation av första graden
- u' = F(u,t),
genom att sätta ui = x(i).
Vanligtvis finns det också ett begynnelsevärdesvilkor u(t0) = u0.
Existens och entydighet
För att garantera existensen av lösningar till
i något intervall kring t0 räcker det att F är kontinuerlig.
För att lösningen ska vara entydig krävs det ytterligare vilkor varav det mest använda är att F är Lipschitzkontinuerlig i den första variabeln.
Klassifikation av ODE:er
ODEn u' = F(u,t) sägs vara autonom om F inte beror på t, dvs u' = F(u).
Ekvationen sägs vara lineär om F(u,t) = A(t)u + b(t) där A(t) är en matrisvärd funktion och b har samma dimensioner som u.
Sturm-Liouville teori
Sturm-Liouvilles teori är en generell metod för lösning av andra ordningens linjära differentialekvationer med variabla koefficienter.
Bibliografi
- A. D. Polyanin and V. F. Zaitsev, Handbook of Exact Solutions for Ordinary Differential Equations (2nd edition)", Chapman & Hall/CRC Press, Boca Raton, 2003. ISBN 1-58488-297-2
- A. D. Polyanin, V. F. Zaitsev, and A. Moussiaux, Handbook of First Order Partial Differential Equations, Taylor & Francis, London, 2002. ISBN 0-415-27267-X
- D. Zwillinger, Handbook of Differential Equations (3rd edition), Academic Press, Boston, 1997.
- Hartman, Philip, Ordinary Differential Equations, 2nd Ed., Society for Industrial & Applied Math, 2002. ISBN 0-89871-510-5.
- W. Johnson, A Treatise on Ordinary and Partial Differential Equations, John Wiley and Sons, 1913, in University of Michigan Historical Math Collection
- E.L. Ince, Ordinary Differential Equations, Dover Publications, 1958, ISBN 0-486-60349-0
- Witold Hurewicz, Lectures on Ordinary Differential Equations, Dover Publications, ISBN 0-486-49510-8