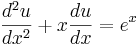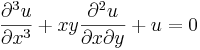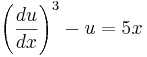Linjär differentialekvation

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Med linjär differentialekvation menas en differentialekvation där den sökta funktionen och dess derivator endast uppträder linjärt.

Lösning av linjära differentialekvationer

Att lösa en differentialekvation innebär att finna en funktion som uppfyller ekvationen. Då differentialekvationen är inhomogen skiljer man på partikulärlösningen och den homogena lösningen.

Exempel

Linjär, andra ordningens ekvation:

\frac{d^2 u}{d x^2}+x\frac{d u}{d x}=e^x

Linjär, tredje ordningens ekvation i två variabler:

\frac{\part^3 u}{\part x^3}+xy\frac{\part^2 u}{\part x \part y} +u=0

Olinjär, första ordningens ekvation:

\left(\frac{d u}{d x}\right)^3-u=5x
Hämtad från "https://sv.rilpedia.org/wiki/Linj%C3%A4r_differentialekvation"
Personliga verktyg