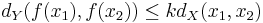Kontraktionsavbildning
Från Rilpedia
Kontraktionsavbildning, inom matematiken en avbildning där avståndet mellan två punkter före avbildningen är större än avståndet mellan dem efter avbildningen. Avbildningarna aktualiserades i slutet av 1980-talet, speciellt i form av itererande funktionssystem, eftersom de kan representera bilder med naturliga utseenden.
Definition
En avbildning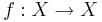 
kallas för kontraktionsavbildning för det metriska rummet X med metriken d, om för alla 
,
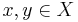för en reell konstant 0 < k < 1.
Man kan definiera en kontraktionsavbildning mellan två olika metriska rum, (X,dX) och (Y,dY), som en avbildning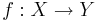 
där det finns ett k, 0 < k < 1, så att för alla x1,x2 i X:
Egenskaper
Varje kontraktionsavbildning är Lipschitzkontinuerlig och därmed även likformigt kontinuerlig.
En viktig egenskap för kontraktionsavbildningar är att det finns exakt en punkt xf som är invariant under avbildning f(xf) = xf. Givet en avbildning f, så kommer alla punkter att transformeras till denna punkt (Banachs fixpunktssats) Detta betyder att om punkten xf representerar en av alla möjliga bilder i "bildmängden" X, finns det en avbildning f(x) som kan representera bilden. Problemet är då att finna den rätta kontraktionsavbildningen som kan reproducera bilden.
