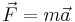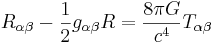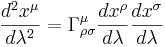Allmänna relativitetsteorin
Från Rilpedia

Den allmänna relativitetsteorin är en teori om gravitation som publicerades av Albert Einstein 1915. Den förenar den speciella relativitetsteorin och Isaac Newtons universella gravitation genom idén att gravitationen inte är en kraft i klassisk fysikalisk mening, utan är en manifestation av rumtidens geometri. Rumtiden är inte plan, utan krökt, och krökningen påverkar hur kroppar färdas genom rumtiden. Denna krökning bestäms av energins och materiens fördelning i rummet.
Innehåll |
Inledning
Fram till början av 1900-talet dominerade Isaac Newtons föreställningar om tid och rum. Universum antogs vara oändligt i alla riktningar och oändligt i tiden samt i stor skala oföränderligt. Detta medförde problem. Vad kunde hindra den attraherande gravitationskraften från att destabilisera varje form av fördelning av materien? Newton antog (oriktigt) att materiens fördelning på något sätt var sådan att en destabilisering undveks. Astronomen Olbers ställde frågan (Olbers paradox): Varför är natthimlen mörk? Om universum är oändligt så borde i varje riktning finnas ett ljust objekt, en stjärnyta. Den allmänna relativitetsteorin är grundläggande för att besvara frågor inom kosmologin.
Den i dag allmänt accepterade föreställningen om universums ursprung och utveckling kallas Big Bang och innebär att universum ursprungligen var koncentrerat i en extremt het massa av ytterst hög täthet. Under miljarder år har sedan universum expanderat och materia bildat stjärnor och galaxer. Universums expansiva kraft motverkas av gravitationen som bromsar universums expansion. Gravitationens styrka är en av de faktorer som bestämmer universums framtid. Den ryske fysikern Alexander Friedmann använde år 1922 allmänna relativitetsteorin för att finna en modell som beskrev universums utveckling. Enligt denna modell bromsas universums expansion för att sedan övergå i en sammandragning. Han grundade sin modell på antagandet att i stor skala är universum likformigt i varje riktning sett från varje utgångspunkt.
I starka gravitationsfält kan gravitationen manifestera sig som en optisk "störning", infallande ljus böjs och en stor massa kan fungera som en lins, en "gravitationslins". Inom astronomin kan detta utnyttjas för att observera objekt som annars skulle vara skymda. Ljus kan tjäna som en "sond" för rummets avvikelser från det "rätlinjiga" då ljusets hastighet är den högsta som kan förekomma, vilket innebär att ljuset följer de kortast möjliga banorna.
Gravitation ger också upphov till tidsdilatation. En klocka går långsammare jämfört med en klocka som befinner sig i ett område med svagare gravitation. En konsekvens av detta är att GPS-satelliternas atomklockor måste korrigeras för skillnaden i gravitation mellan satelliternas banor och jordytan.
Ett fenomen som hänger nära ihop med tidsdilatationen är den frekvensförskjutning av ljus som orsakas av gravitation. Frekvensen hos en ljussignal som sänds från en punkt med starkare gravitation än den punkt där ljuset mottages kommer att där uppfattas som "rödförskjutet", ha en lägre frekvens jämfört med vad en observatör på sändarsidan skulle anse.
Den som saknar bakgrundskunskaper om relativitet rekommenderas att först läsa artikeln om speciella relativitetsteorin.
Historik
Isaac Newton antog att objekt hade en absolut hastighet och att vissa objekt verkligen befann sig i vila medan andra verkligen var i rörelse. Han insåg att det inte finns något sätt att mäta dessa absoluta hastigheter. Newton trodde dock att hans teori var orimlig utan antagandet att det finns absoluta referenspunkter även om de inte kan fastställas. För rotationer anförde han den roterande vattenspannen som ett exempel på absolut rörelse. Om vi kan iaktta en konkav vattenyta är det möjligt att påstå att spannen roterar i en absolut mening.
På 1800-talet formulerade James Clerk Maxwell en uppsättning ekvationer – Maxwells fältekvationer – som visade att ljus beter sig som en elektromagnetisk våg som färdas med konstant hastighet genom rummet (som fortfarande kunde antas vara absolut, innehålla en "eter" som medium för ljusets utbredning). Detta tycktes innebära ett sätt att undvika problemen med Newtons relativitet. Genom att mäta ljushastigheten för ljus utsänt från objekt i olika rörelsetillstånd skulle dessa objekts hastighet relativt det absoluta rummet kunna fastställas. Försök gjorda av Michelson och Morley mot slutet av 1800-talet gav dock det entydiga resultatet att ljusets hastighet var oberoende av dessa rörelsetillstånd.
Einstein kom på teoretisk väg fram till detta resultat, som han publicerade 1905 i sin uppsats Zur Elektrodynamik bewegter Körper (Om elektrodynamiken hos kroppar i rörelse).
Den speciella relativitetsteorin (formulerad av Albert Einstein 1905) utgick från postulatet att ljusets hastighet är densamma för alla observatörer. Den gjorde mekanikens ekvationer konsistenta med avseende på observationer gjorda av observatörer i likformig relativ rörelse, vilket krävde att avstånd och tid var variabla, var olika för olika observatörer. Det var därmed inte längre möjligt att betrakta rum och tid som åtskilda utan endast som delar av ett enhetligt fyrdimensionellt system, en "rumtid".
Speciella relativitetsteorin behandlar system som befinner sig i likformig relativ rörelse. Enligt teorin finns det inget sätt att avgöra att något sådant system skulle ha en särställning. Det finns därför inte någon meningsfull tolkning av påståendet att ett system "är i vila". Det är detta förhållande som ordet relativitet syftar på. Det är inte möjligt att på ett fysikaliskt meningsfullt sätt tala om ett objekts hastighet och acceleration utan att först välja en referensram, definiera ett koordinatsystem i rummet, som objektets rörelse relateras till.
Den allmänna relativitetsteorin kombinerar relativitet med ekvivalensprincipen, nämligen principen att man i ett lokalt system inte kan särskilja effekterna av gravitation och likformig acceleration. Detta leder till att rumtidens geometri beror på förekomsten av materia och energi: materia/energi ger upphov till en krökt rumtid. Partiklar som färdas fritt i denna krökta rumtid rör sig därmed under inflytande av gravitationen som inte längre kan anses vara en kraft utan är en egenskap hos rummet. Gravitationen är universell i den meningen att den påverkar alla kroppar på samma sätt, till skillnad från andra krafter som till exempel den elektromagnetiska kraften.
Allmänna relativitetsteorin kan tillämpas på många fenomen såsom ljusböjning i starka gravitationsfält, svarta hål, universums expansion och Big Bang.
Teorins grunder
Icke-Euklidisk geometri
En av grunderna för teorin är utvecklingen av icke-euklidiska geometrier under 1800-talets senare hälft. Euklidisk geometri kan sägas kännetecknas av Euklides femte axiom, parallellaxiomet, det vill säga att parallella linjer saknar skärningspunkt (är ekvidistanta). Janos Bolyai och Carl Friedrich Gauss insåg att ett postulat innebärande att parallella linjer är ekvidistanta inte nödvändigtvis måste gälla som grund för en korrekt beskrivning av verkligheten. Gauss utförde också mätningar av trianglars vinkelsummor för punkter på kilometervisa avstånd (för en icke-euklidisk geometri skulle denna summa avvika från 180 grader) men rumskrökningen vid jordytan är för liten för att kunna påvisas i ett sådant experiment. Allmänna icke-euklidiska geometrier formulerades av Gauss's elev Bernhard Riemann. Den moderna formuleringen av teorin använder sig av differentialgeometri, som är en gren av matematiken där man studerar lokala egenskaper hos en typ av mycket generella strukturer som kallas differentierbara mångfalder.
Den speciella relativitetsteorin
I den speciella relativitetsteorin spelar inertialsystem en viktig roll. Inertialsystem är referenssystem som befinner sig i likformig rörelse och som inte påverkas av gravitation (det betyder inte att man inte kan ta med krafter och accelerationer i beräkningarna, men dessa måste behandlas för sig).
Den speciella relativitetsteorin utgår från att alla inertialsystem är ekvivalenta (samma fysikaliska lagar gäller i samtliga) och från postulatet att ljushastigheten är densamma i alla inertialsystem. Skälet till att den kallas speciell är att den inte behandlar gravitationen.
Ekvivalensprincipen
Einstein utgick från det som numera kallas den svaga ekvivalensprincipen. Enligt denna är den massa som ingår i Newtons andra lag
identisk med den massa som ingår i den gravitationella kraften
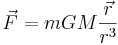 ,
,
vilket innebär att man kan definiera en acceleration på grund av gravitationen,
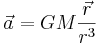 .
.
Den svaga ekvivalensprincipen kan därför formuleras på ett annat sätt: fritt fallande objekt beter sig på samma sätt under påverkan av likformig acceleration som under påverkan av gravitation. Man måste dock begränsa sig till så små regioner av rummet att gravitationskraften kan anses konstant.
Svaga ekvivalensprincipen brukar ofta illustreras med tankeexperimentet att en observatör som befinner sig i en sluten hiss i rymden inte kan avgöra, genom att observera fallande objekt inuti hissen, om hissen accelererar likformigt på grund av en konstant kraft från hisslinan eller om den påverkas av gravitation (ingen kraftverkan från hisslinan).
I accelererande referensramar har fritt rörliga kroppar en acceleration med avseende på denna referensram, det vill säga det finns en kraft som härrör från referensramens acceleration och inte från direkt påverkan av yttre objekt (till exempel känner vi G-krafter i kurvor när vi färdas med bil). Analogt uppstår corioliskrafter och centripetalkrafter med avseende på vissa referensramar för roterande objekt som jorden eller en karusell.
Einstein generaliserade denna princip till det som nu kallas Einsteins ekvivalensprincip (EEP): I en tillräckligt liten region av rumtiden är det omöjligt att särskilja gravitation och acceleration med något lokalt experiment. I en sådan lokal region kan den speciella relativitetsteorin tillämpas.
Einstein visade hur EEP leder till att gravitationen inte längre kan anses vara en kraft utan istället är en effekt av det krökta rummet. I den speciella relativitetsteorin kan en acceleration unikt definieras i förhållande till ett inertialsystem. Om till exempel en elektriskt laddad partikel accelereras av ett elektriskt fält så kan man unikt mäta accelerationen relativt ett system i likformig rörelse; det är bara likformig rörelse som är relativ. Men om gravitationen behandlas som en acceleration hamnar vi i svårigheter eftersom det inte finns några objekt som inte påverkas av gravitationen. Det finns alltså ingenting relativt vilket vi kan mäta denna acceleration! Einstein såg detta som ett så allvarligt problem att han bestämde sig för att helt överge idén att gravitationen är en kraft och därmed att det finns något sådant som gravitationell acceleration.
Fritt fallande referenssystem
I den allmänna relativitetsteorin talar man om fritt fallande referenssystem. Dessa är oaccelererade system som rör sig fritt, utan påverkan från yttre krafter. Objekt som endast är under inflytande av gravitation är fritt fallande och följer därmed den kortast möjliga banan mellan punkter i rumtiden. Detta är det stora steget när man går från den speciella till den allmänna relativitetsteorin.
Eftersom det gravitationella fältet från ett massivt objekt aldrig är konstant i rummet kan man inte definiera globala referenssystem som omfattar hela rummet. Om man försöker göra detta kommer fritt fallande objekt som är tillräckligt långt borta att förefalla accelererade när de påverkas av gravitationen. (Antag att två objekt attraheras gravitationellt av en planet på långt avstånd från denna och faller radiellt mot planeten, vilket går att skilja från likformig acceleration av det globala referenssystemet.)
Man måste därför nöja sig med lokala inertialsystem, vilket leder till att de relativa hastigheterna hos objekt på stort avstånd från varandra inte är väldefinierade.
Det krökta rummet
Rumtiden får alltså en krökt geometri där Newtons lagar antas gälla i lokala referensramar för låga hastigheter. Fria partiklar färdas längs räta linjer i dessa lokala inertialsystem men när dessa sträckor kan anses "långa" märks krökningen av rummet. Partiklarna färdas då efter geodetiska banor, det vill säga de kortaste banorna i det krökta rummet. Detta kan tolkas som att Newtons första lag ersätts med lagen om geodetisk rörelse.
Det är naturligt att matematiskt beskriva detta med differentierbara mångfalder, vilka är matematiska strukturer som är lokalt plana. Mer precist ser en n-dimensionell mångfald lokalt (på infinitesimala avstånd) ut som Rn, det vill säga det euklidiska n-dimensionella rummet. I den allmänna relativitetsteorin ser rummet lokalt ut som det plana Minkowskirummet som används i den speciella relativitetsteorin, men globalt är det krökt. På grund av detta kan man inte direkt jämföra vektorer som hastighet och acceleration för olika punkter i rummet utan vektorer för olika punkter tillhör olika tangentrum.
Sammanfattning
I den speciella relativitetsteorin antas att referensramar kan utvidgas obegränsat i tid och rum. I den allmänna relativitetsteorin kan vi däremot endast definiera lokala referensramar, det vill säga referensramar definierade i en tillräckligt liten del av rumtiden. Detta är analogt med att vi kan rita en tvådimensionell karta av ett litet område av jordytan med stor noggrannhet, men inte utsträcka kartan till att avbilda hela jordytan utan förvrängning.
Den allmänna relativitetsteorin vilar på tre principer:
- Gravitationen är inte en kraft utan en effekt av att rumtiden är krökt.
- Alla fria objekt rör sig efter de kortaste möjliga banorna i detta krökta rum. Dessa kortaste banor kallas geodeter.
- Krökningen av rummet är en effekt av massa och energi.
Experimentellt stöd
Det första experimentella stödet för den allmänna relativitetsteorin gavs av Arthur Eddington som 1919 företog en expedition för att mäta ljusstrålars böjning på grund av solens gravitation och sedan jämföra dessa med den allmänna relativitetsteorins förutsägelser. Under en total solförmörkelse registrerade Eddington stjärnpositioner fotografiskt i solens omedelbara närhet för att sedan jämföra dessa positioner i riktningar utan solens påverkan och han kunde på så sätt visa att ljusbanorna böjdes av i gravitationsfältet nära solen. I vilken utsträckning Eddington verkligen gav ett vetenskapligt stöd för den allmänna relativitetsteorin är omdiskuterat. Senare undersökningar (observationmaterialet är bevarat) tyder på att endast själva ljusböjningsfenomenet blev fastställt med någorlunda säkerhet.
Moderna experiment har verifierat teorin inom gränserna för experimentens noggrannhet. Exempelvis påvisade Pound-Rebkaexperimentet (1959) ändringar i våglängd för ljus från en koboltkälla över en sträcka av 22,5 meter i en riktning motsatt gravitationens. Merkurius perihelionprecession är ett annat exempel.
Den allmänna relativitetsteorins status
Den allmänna relativitetsteorin betraktas i dag som en "effektiv" teori för låga energier (den anses asymptotiskt korrekt vid låga energier). För höga energier är den oförenlig med kvantmekaniken. Bland annat strängteorin är ett försök att förena gravitation och kvantmekanik i en enhetlig teori (se kvantgravitation).
Matematisk beskrivning
Matematiskt modelleras rumtiden med hjälp av differentialgeometri som en fyrdimensionell pseudo-Riemannsk mångfald, (jfr engelskans "manifold") med en metrik, eller metrisk tensor, 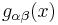 , som specificerar rummets lokala krökning i punkten
, som specificerar rummets lokala krökning i punkten 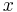 . Metriken beskriver hur man mäter avstånd på mångfalden – man kan säga att den anger avvikelsen från Pythagoras sats för trianglar i det icke-Euklidiska rummet – och är en symmetrisk 2-tensor definierad över den 4-dimensionella rumtiden (det vill säga den kan representeras som en 4 x 4 – matris), vilket innebär att den har 10 oberoende komponenter.
. Metriken beskriver hur man mäter avstånd på mångfalden – man kan säga att den anger avvikelsen från Pythagoras sats för trianglar i det icke-Euklidiska rummet – och är en symmetrisk 2-tensor definierad över den 4-dimensionella rumtiden (det vill säga den kan representeras som en 4 x 4 – matris), vilket innebär att den har 10 oberoende komponenter.
Einsteins fältekvationer anger att mångfaldens krökning, som anges av den så kallade Riemanntensorn, i en punkt är direkt relaterad till stressenergitensorn i denna punkt. Denna tensor är ett mått på materia/energi-densiteten. Metriken i sin tur är relaterad till Riemanntensorn. Rumtid-krökningen styr hur materia rör sig och materia styr hur rumtiden kröks.
Einsteins fältekvationer specificierar alltså rumtidens respons på förekomsten av materia och energi. De innefattar tensorer och kan skrivas
vilket motsvarar en ickelinjär differentialekvation för varje komponent av den metriska tensorn 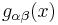 . Högerledet i denna ekvation specifierar mass-energifördelningen i rumtiden, och relaterar detta till vänsterledet som ger ett mått på krökningen.
. Högerledet i denna ekvation specifierar mass-energifördelningen i rumtiden, och relaterar detta till vänsterledet som ger ett mått på krökningen.
I ekvationen ovan är
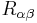 Riccis krökningstensor,
Riccis krökningstensor,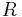 skalärkrökningen,
skalärkrökningen,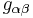 den metriska tensorn,
den metriska tensorn,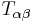 stressenergitensorn,
stressenergitensorn,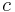 ljusets hastighet och
ljusets hastighet och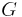 gravitationskonstanten som också förekommer i Newtons gravitationslag.
gravitationskonstanten som också förekommer i Newtons gravitationslag.
På grund av att metriken har 10 komponenter är Einsteins ekvationer därför 10 till antalet, en för varje komponent. De matematiska egenskaperna hos mångfalder ger dock den så kallade Bianchi-identiteten som ger restriktioner på fyra av komponenterna, motsvarande rumtidens fyra koordinater. Alltså återstår 6 oberoende ekvationer.
Riccitensorn 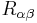 och skalärkrökningen
och skalärkrökningen 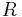 beräknas från den mer generella Riemanntensorn, vilken in sin tur beräknas från metriken och derivator av denna.
beräknas från den mer generella Riemanntensorn, vilken in sin tur beräknas från metriken och derivator av denna.
Materiens respons på den krökta rumtiden i sin tur ges av att en fri partikels bana följer en geodet, en parametriserad kurva 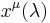 som är den kortaste sträckan i den krökta rumtiden, och ges av den geodetiska ekvationen
som är den kortaste sträckan i den krökta rumtiden, och ges av den geodetiska ekvationen
där man summerar över index ρ och σ enligt Einsteins summakonvention. 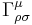 är den så kallade Christoffelsymbolen som också är relaterad till rummets krökning.
är den så kallade Christoffelsymbolen som också är relaterad till rummets krökning.
Einsteins fältekvationer skrivs ibland med en parameter kallad "den kosmologiska konstanten", Λ, som ursprungligen introducerades av Einstein för att vara konsistent med ett statiskt universum (som varken expanderar eller drar sig samman). Denna åtgärd var oriktig av två anledningar. Ett statiskt universum beskrivet av denna teori är instabilt och observationer gjorda av Edwin Hubble ett årtionde senare visade att vårt universum inte är statiskt utan expanderar. Parametern Λ övergavs därför. På senare tid har man genom observationer upptäckt att ett värde på Λ skilt från noll ändå är nödvändigt. Detta värde leder istället till att universums expansion accelererar.
Fältekvationen med kosmologisk konstant skrivs:
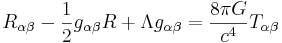 .
.
Se vidare kosmologiska konstanten för den fysikaliska innebörden av Λ.
Litteratur
Populärt
- Kip Thorne, Black Holes and Time Warps: Einstein's Outrageous Legacy, (W.W. Norton & Company, New York, 1994). ISBN 0-393-31276-3. Prisbelönt populärvetenskap.
- Hermann Bondi, Relativity and Common Sense, Heinemann (1964). ISBN 0-486-24021-5. En lätt introduktion till principerna bakom relativiteten av en välkänd fysiker.
Med matematik
I allmänhet behöver man som förkunskaper en del linjär algebra (bland annat matriser), analys och klassisk mekanik (på högre nivå tensorer och lagrangeformuleringen av mekaniken) för att studera allmän relativitetsteori. Flera av böckerna nedan förklarar dock mycket av detta och den differentialgeometri man behöver introduceras i dessa böcker. I själva verket behöver man inte kunna så mycket modern fysik för att förstå teorin. Det är dock bra att ha grundkunskaper om den speciella relativitetsteorin innan man börjar.
På svenska:
- Olof Sjöstrand, Einsteins relativitetsteori - Matematisk bakgrund och enkla tillämpningar, Akademiförlaget (1971). Börjar med den speciella relativitetsteorin. Differential- och integralkalkyl, partiella derivator, differentialekvationer och determinanter bör vara kända för att fatta den gradvisa introduktionen av den tensoranalys som används för den allmänna teorin.
På engelska:
- Sean Carroll, A no-nonsense introduction to general relativity (pdf). Mycket kortfattad (20 sidor) men användbar introduktion till teorin på universitetsnivå. Ger en indikation om vad man behöver lära sig.
- Ray D'Inverno, Introducing Einstein's Relativity, (Oxford University Press, 1993). En modern text på "undergraduate level", det vill säga enklare universitetsnivå.
- James B. Hartle, Gravity: An Introduction to Einstein's General Relativity (2002), ISBN 0-8053-8662-9. Också "undergraduate" universitetsnivå, men betonar fysiken mer än matematiken – de flesta andra böcker börjar med differentialgeometri och kommer sedan till fysiken.
- Bernard F. Schutz, A First Course in General Relativity (1995), ISBN 0-521-27703-5. Ungefär samma nivå men börjar med matematiken.
- Sean M. Carroll, Spacetime and Geometry: An Introduction to General Relativity (2003), ISBN 0-8053-8732-3. Något högre nivå än de tre tidigare. Finns även i en tidigare, något kortare version på nätet: Introduction to general relativity.
- Jerzy Plebanski & Andrzej Krasinski, An Introduction to General Relativity and Cosmology. Cambridge University Press ( July 2006), ISBN 0-521-85623-X. En modern första "graduate textbook".
- Misner, Thorne, Wheeler: Gravitation, Freeman (1973), ISBN 0-7167-0344-0. En klassisk bok på relativt hög nivå, kräver en del matematik och fysik på högre universitetsnivå ("graduate level", det vill säga. doktorandnivå). Mycket omfattande; baserar sig till större del på geometriska grunder och resonemang.
- W. Perret and G.B. Jeffrey, trans.: The Principle of Relativity: A Collection of Original Memoirs on the Special and General Theory of Relativity, New York Dover (1923).
På tyska:
- Albert Einstein: Die Grundlage der allgemeinen Relativitätstheorie. In: Annalen der Physik. 49, 1916, S. 769–822 (Faksimile, PDF)
- Albert Einstein: Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes. In: Annalen der Physik. 35, 1911, S. 898–908 (Faksimile, PDF)
- Albert Einstein: Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie. In: Sitzungsberichte der Preußischen Akademie der Wissenschaften. 1915, S. 831–839
Se även