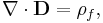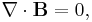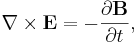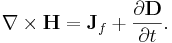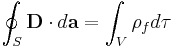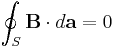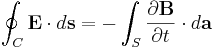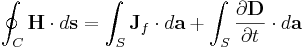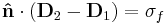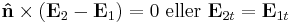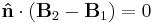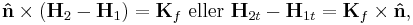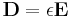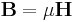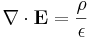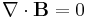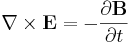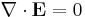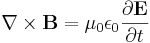Maxwells ekvationer

Från Rilpedia

(Omdirigerad från Maxwells fältekvationer)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
För de termodynamiska relationer som också bär Maxwells namn, se Maxwellrelationer.

Maxwells elektromagnetiska ekvationer är fyra partiella differentialekvationer som sammanställdes av James Clerk Maxwell och beskriver elektriska och magnetiska fält.

Innehåll

Sammanfattning

Generell form

Maxwells ekvationer på vanlig form uttrycks med fyra ekvationer


\nabla \cdot \mathbf{D} = \rho_f,


\nabla \cdot \mathbf{B} = 0,


\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}} {\partial t},


\nabla \times \mathbf{H} = \mathbf{J}_f + \frac{\partial \mathbf{D}} {\partial t}.


Den första ekvationen (Gauss lag), beskriver hur elektriska fält uppstår från elektriska laddningar; den andra ekvationen beskriver att det inte finns "magnetiska laddningar", så kallade magnetiska monopoler; den tredje ekvationen (Faradays induktionslag) beskriver hur elektriska fält uppstår från variationer i magnetiska fält och den fjärde ekvationen (Ampères lag med Maxwells korrektion) beskriver hur magnetiska fält uppstår från variationer i elektriska fält.

Lista över de ingående storheterna

E: Elektriska fältet

D: Elektriska flödestätheten.

H: Magnetfältet¹

B: Magnetiska flödestätheten¹.

Jf: fria strömmen av laddningstäthet.

¹Detta kommer ur en äldre konvention, och idag kallas båda ofta "magnetfält".

Subskriptet f används här för att notera de fria laddningarna; de bundna laddningarna finns medräknade i E och D-fälten.

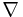\nabla kallas nabla och används som deriveringssymbol i vektoranalysen.

Integralform

Ekvationerna kan även uttryckas på integralform:

\oint_S \mathbf{D}\cdot d\mathbf{a} = \int_V \rho_f d\tau
\oint_S \mathbf{B}\cdot d\mathbf{a} = 0
\oint_C \mathbf{E}\cdot d\mathbf{s} = -\int_S {\part \mathbf{B} \over \part t} \cdot d\mathbf{a}
\oint_C \mathbf{H}\cdot d\mathbf{s} = \int_S\mathbf{J}_f\cdot d\mathbf{a} + \int_S{\part \mathbf{D} \over \part t}\cdot d\mathbf{a}

Randvärdesvillkor

Vid övergången från medium 1 till medium 2 ger Maxwells ekvationer:

\mathbf{\hat{n}}\cdot (\mathbf{D}_2 - \mathbf{D}_1) = \sigma_f
\mathbf{\hat{n}}\times(\mathbf{E}_2 - \mathbf{E}_1) = 0 \mbox{ eller }\mathbf{E}_{2t} = \mathbf{E}_{1t}
\mathbf{\hat{n}}\cdot(\mathbf{B}_2 - \mathbf{B}_1) = 0
\mathbf{\hat{n}}\times(\mathbf{H}_2 - \mathbf{H}_1) = \mathbf{K}_f \mbox{ eller } \mathbf{H}_{2t} - \mathbf{H}_{1t} = \mathbf{K}_f\times\mathbf{\hat{n}},

där Kf är den fria ytströmtätheten.

Superpositionsprincipen

M:s ekvationer är linjära partiella differentialekvationer. Detta betyder att om två eller fler elektromagnetiska fält är lösningar till ekvationerna, så är summan av dem också en lösning. Detta brukar benämnas superpositionsprincipen (läs artikeln om superpositionsprincipen).

Linjära medier eller material

I linjära medier är den makroskopiska fältstyrkan D och H proportionellt relaterade till fältstyrkorna E och B

\mathbf{D} = \epsilon \mathbf{E}
\mathbf{B} = \mu \mathbf{H}

I linjära och isotropiska medier är permittiviteten ε och permeabiliteten μ konstanta och Maxwells ekvationer reduceras till

\nabla \cdot \mathbf{E} = \frac{\rho} {\epsilon}
\nabla \cdot \mathbf{B} = 0
\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}} {\partial t}
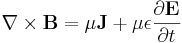\nabla \times \mathbf{B} = \mu \mathbf{J} + \mu \epsilon \frac{\partial \mathbf{E}} {\partial t}.

Många material kan med god approximationsgrad betraktas som linjärt isotropiska.

Vakuum

Vakuum är ett linjärt isotropiskt medium och proportionalitetskonstanterna betecknas vanligtvis ε0 samt μ0. Om det inte finns några strömmar eller elektriska laddningar i vakuumet kan Maxwells ekvationer förenklas till

\nabla \cdot \mathbf{E} = 0
\nabla \cdot \mathbf{B} = 0
\nabla \times \mathbf{E} = -\frac{\partial\mathbf{B}} {\partial t}
\nabla \times \mathbf{B} = \mu_0 \epsilon_0 \frac{\partial \mathbf{E}} {\partial t}

Dessa ekvationer har enkla lösningar i formen av en framåtskridande sinusformad plan elektromagnetisk våg, med elektriska och magnetiska fältriktningarna vinkelräta mot varandra och till fortplantningsriktningen. Fälten är i fas och transporteras med hastigheten

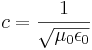c = \frac{1}{\sqrt{\mu_0 \epsilon_0}} .

Våghastigheten och ljushastigheten

Maxwell konstaterade att att de elektriska och magnetiska proportionalitetskonstanterna, ε0 och μ0, med experimentella värden och sorter insatta i ovanstående formel, gav en hastighet c som stämde väl med ljushastighetens experimentellt kända värde i vakuum. Den så förutsedda elektromagnetiska strålningen var på Maxwells tid okänd i praktiken. Men hur den än kunde se ut så skulle den alltså utbreda sig med ljusets hastighet. Och omvänt skulle ljuset vara en elektromagnetisk strålning. Strålningens existens och egenskaper bekräftades senare av Heinrich Hertz.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Maxwells_ekvationer"
Personliga verktyg