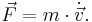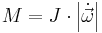Tensor

Från Rilpedia

(Omdirigerad från Tensoranalys)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

En tensor (lat. tendo, "spänna, dra åt, tänja") är ett matematiskt objekt som är en generalisering av begreppen skalär, vektor och linjär operator. Tensorer är betydelsefulla inom differentialgeometri, fysik och teknik. Formalismen utvecklades av Gregorio Ricci-Curbastro omkring 1890 under benämningen absolut differentialkalkyl. Einsteins allmänna relativitetsteori, utvecklad under 1910-talet, formuleras med hjälp av tensornotation, och inom kontinuummekaniken används exempelvis spänningstensorn. Tensorer har tillkommit som ett praktiskt verktyg för att beskriva flerdimensionella objekt. Med tensorer hanteras sådana objekt mycket enklare än i utskriven komponentform.

Innehåll

1 Definition
2 Tensorer i fysiken
3 Tensorer som generalisering av skalärer, vektorer och matriser
4 Tensorer som indexerade storheter
5 Tensorer som multilinjärformer
6 Tensorordning
7 Se även

Definition

Man kan tänka sig att tensorer representerar ett schema av tal som bestämmer hur de individuella elementen skall kombineras vid multiplikation, addition, och dylikt. En tensor sägs ha ordning n, där n är ett naturligt heltal 0, 1, 2, och så vidare och ordningen betecknar antalet index ett element identifieras med.

Det finns två sätt att närma sig definitionen av tensorer, som kallas det klassiska (eller fysikaliska) sättet och det moderna (eller matematiska) sättet.

Det klassiska eller fysikaliska sättet att definiera tensorer i termer av objekt vars komponenter transformeras enligt speciella regler och som även introducerar nya idéer om kovarianta och kontravarianta transformationer.

Synsättet innebär att man betraktar tensorer som multidimensionella arrayer som är n-dimensionella generaliseringar av skalärer, 1-dimensionella vektorer och 2-dimensionella matriser. Tensorns "komponenter" är arrayens index.

Betraktelsesättet kan även generaliseras till tensorfält där elementen i tensorn är funktioner eller till och med differentialer. Det senare innebär en utvidgning av idéerna kring Jacobianen, det vill säga att elementen är derivator av en viss funktion.

Det moderna eller matematiska sättet som innebär att speciella vektorrum definieras oberoende av koordinatsystemet förrän baser introduceras.

Det innebär att tensorer huvudsakligen är abstrakta objekt, som uttrycks som termer av ändliga multilinjära koncept. Tensoregenskaperna, eller "manipulationsreglerna", kan då härledas från definitionerna av linjära avbildningar; en mer generell härledning baseras på utvidgningar av linjär algebra till multilinjär algebra.

Tensorer i fysiken

Många fysikaliska lagar är proportionaliteter. Till exempel medför en kraft som verkar på en kropp (fysik) en hastighetsförändring som är proportionell mot kraften:

$\vec F=m\cdot\dot{\vec v}.$

Denna ekvation utsäger också att kraftens riktning även blir accelerationens riktning. Samma proportionalitetsfaktor, massan $m$ , dyker också upp i formeln för kinetisk energi

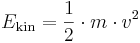$E_\mathrm{kin}=\frac12\cdot m\cdot v^2$ .

Det finns dock sammanhang som inte låter sig beskrivas på detta sätt, eftersom deras proportionalitetsfaktorer är beroende på de ingående vektorernas riktningar. Ett exempel är vridningsrörelse: Om ett vridmoment verkar på en roterande kropp medför det en ändring av kroppens vinkelhastighet, och en fördubbling av vridmomentet medför en fördubbling av denna effekt. Det gäller alltså att

$M=J\cdot\left|\dot{\vec\omega}\right|$

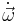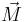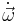med en proportionalitetsfaktor $J$ , som kan vara olika beroende på riktningen av $\dot{\vec\omega}$ . Riktningarna på $\vec M$ och $\dot{\vec\omega}$ behöver inte heller stämma överens. Rotationsenergin kan på samma sätt framställas med en riktningsberoende proportionalitetsfaktor $J$ som

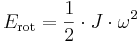$E_\mathrm{rot}=\frac12\cdot J\cdot\omega^2$ .

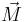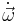Detta riktningsberoende betyder att tröghetsmomentet $J$ är en tensoriell storhet, i detta fall en tensor av andra ordningen, tröghetstensorn. "Andra ordningen" innebär i detta fall, att två vektorer är inblandade, i första formeln $\vec M$ och $\dot{\vec\omega}$ , i den andra formeln vektorn 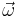$\vec\omega$ två gånger. Tensorer av andra ordningen kan alltså grovt sagt göra nya vektorer av vektorer eller göra tal av vektorpar. Matematiskt motsvarar det en linjär avbildning respektive en bilinjär form, som bägge kan uttryckas med en 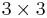$3\times3$ -matris. Räknemässigt är en tensor av rang 2 alltså inget annat än en (kvadratisk) matris, och formlerna ovan får formen

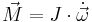$\vec M=J\cdot\dot{\vec\omega}$ respektive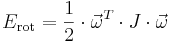 $E_\mathrm{rot}=\frac12\cdot\vec\omega^T\cdot J\cdot\vec\omega$

med motsvarande matris $J$ .

Tensorer som generalisering av skalärer, vektorer och matriser

I många tillämpningar, till exempel inom elasticitetsteori räcker det att tänka sig tensorer som fortsättningen på följden skalär, vektor, matris. Då skiljer man på tensorer av olika ”ordning” eller ”rang”.

En tensor av nollte ordningen är ett tal, även kallat skalär.
En tensor av första ordningen uttrycks som en vektor (matematik). I det n-dimensionella rummet har en sådan tensor precis n koefficienter.
En tensor av andra ordningen uttrycks med en kvadratisk matris, alltså ett talschema i vilken var och en av tensorns n² koefficienter betecknas med två index. (Exempel: ett kalkylark i ett kalkylprogram; en tvådimensionell pixelbild.)
En tensor av tredje ordningen kan uttryckas med ett kubiskt schema av sina n³ koefficienter, som adresseras med tre index.(Exempel: en mapp med kalkylblad; en videosekvens (pixelbilder med en extra tidskoordinat).
En tensor av m-te ordningen har på motsvarande sätt n^m koefficienter, som man håller reda på med m index.

Tensorer som indexerade storheter

En n-te ordningens tensor är en n-faldigt indexerad storhet 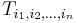$T_{i_1,i_2,...,i_n}$ . Det krävs därvid att det råder ett visst transformationsförhållande. Om sålunda koordinatsystemet vrids med en vridningsmatris $a i, j$ , uttrycks tensorn i de nya koordinaterna som:

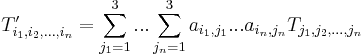$T'_{i_1,i_2,...,i_n}=\sum_{j_1=1}^3 ... \sum_{j_n=1}^3 a_{i_1,j_1} ... a_{i_n,j_n} T_{j_1,j_2,...,j_n}$ .

Tensorer som multilinjärformer

Tensorerna $T$ är multilinjära avbildningar till en kropp $K$ :

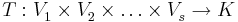$T:V_1^{}\times V_2^{}\times\dots\times V_s^{}\to K$ .

$V_1, \dots\ , V_s$ betecknar här vektorrum över samma kropp $K$ och $s$ betecknar tensorernas ordning.

Multilinjära avbildningar är tensorer, om vart och ett av vektorrummen $V_1, \dots\ , V_s$ antingen är $V *$ eller $V$ .

$V$ är ett godtyckligt vektorrum och $V *$ är dess såkallade duala vektorrum. Ett sådant består av alla linjära avbildningar från vektorrummet $V$ till $K$ , och är självt ett vektorrum av samma dimension och över samma kropp.

Tensorordning

Ordning	Namn	Elementbeteckning	Vanlig transformation^*
0	Skalär	a	S' = \|a\|S \|
1	Vektor	a_i	V'_i = \|a\|a_ijV_j
2	Matris	a_i_j	M'_ij = \|a\|a_ika_jlM_kl
3	Tensor av ordning 3	a_ijk	M'_ijk = \|a\|a_ila_jsa_kmM_lsm

^* |a| är determinanten av koefficientarrayen a_mn eller motsvarande i den givna dimensionen.
Tabell 1. Tensorer av de tre första ordningarna.

Kvantiteter som transformeras enligt kolumn 4 i tabell 1 brukar benämnas tensordensiteter.

Se även

Tensor

Från Rilpedia

Innehåll

Definition

Tensorer i fysiken

Tensorer som generalisering av skalärer, vektorer och matriser

Tensorer som indexerade storheter

Tensorer som multilinjärformer

Tensorordning

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk