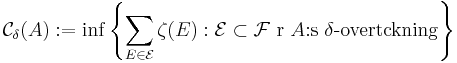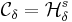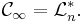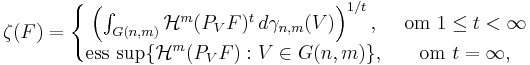Carathéodorys konstruktion
Från Rilpedia
Carathéodorys konstruktionen är en effektiv metod i måtteori för att konstruera Borels yttre mått i metriska rum som kallas yttre Carathéodorymåttet. Metoden uppkallat efter grekisk matematikern Constantin Carathéodory.
Carathéodorys idé var att använda den metriska strukturen så att vi täcka en mängd med vissa testmängder och "mäta" dem med ett testmått. Sedan definierar man måttet på samma sätt som Lebesguemåttet.
Innehåll |
Definitioner
Först behövs några definitioner för konstruktionen. Låt 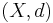 vara ett metriskt rum.
vara ett metriskt rum.
Mängden 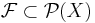 är en testmängdfamilj om det för varje
är en testmängdfamilj om det för varje 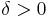 finns mängder
finns mängder 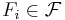 så att
så att
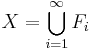 och
och 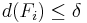 ,
,
för alla 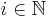 .
. 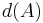 är diametern för
är diametern för 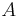 .
.
Låt 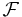 vara en testmängdfamilij. Funktionen
vara en testmängdfamilij. Funktionen ![\zeta : \mathcal{F} \rightarrow [0,\infty]](/w/images/sv.rilpedia.org/math/5/8/0/58073443cdfa90a49ee6e1daf682f4c5.png) är ett testmått om det för varje
är ett testmått om det för varje 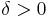 finns en mängd
finns en mängd 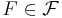 så att
så att
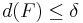 och
och 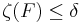 .
.
Om 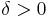 , definierar man att en uppräknelig familj
, definierar man att en uppräknelig familj 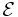 är en
är en 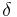 -övertäckning för mängden
-övertäckning för mängden 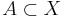 om
om
 och
och 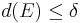
för alla 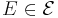 .
.
Konstruktion
Låt 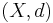 vara ett metriskt rum,
vara ett metriskt rum, 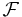 en testmängdfamilij och
en testmängdfamilij och ![\zeta : \mathcal{F} \rightarrow [0,\infty]](/w/images/sv.rilpedia.org/math/5/8/0/58073443cdfa90a49ee6e1daf682f4c5.png) ett testmått.
ett testmått.
För 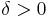 och
och 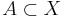 definierar vi
definierar vi
Eftersom 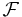 är en testmängdfamilj finns det även en
är en testmängdfamilj finns det även en 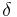 -övertäckning för X. Så att
-övertäckning för X. Så att 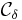 är en funktion
är en funktion
![\mathcal{C}_\delta : \mathcal{P}(X) \rightarrow [0,\infty]](/w/images/sv.rilpedia.org/math/b/7/2/b728f81e92c56a9a743546955a3957db.png) ,
,
som kallas 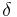 -Carathéodoryinnehållet.
-Carathéodoryinnehållet.
Om 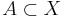 och
och  finns det mindre
finns det mindre 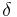 -övertackningar för
-övertackningar för 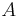 , dvs funktionen
, dvs funktionen 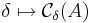 är växande när
är växande när  . Därför existerar gränsvärden
. Därför existerar gränsvärden 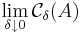 , dvs vi kan definiera gränsfunktionen
, dvs vi kan definiera gränsfunktionen
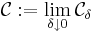 ,
,
som kallas yttre Carathéodorymåttet.
Man kan visa att yttre Carathéodorymåttet är ett Borel yttre mått och om 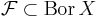 så är yttre Carathéodorymåttet ett Borelregelbundet yttre mått.
så är yttre Carathéodorymåttet ett Borelregelbundet yttre mått.
Exempel
Carathéodorys konstruktion är en mycket effektiv metod, då man kan definiera många naturliga mått med det.
Yttre Hausdorffmått
- Huvudartikel: Hausdorffmått.
Det viktigaste exemplet är det s-dimensionella yttre Hausdorffmåttet. Konstrionen går till så att testmängderna är alla mängder och testmåttet är diametern upphöjat till s.
Mer precist, om 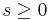 och
och
- metriska rummet
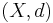 är separabelt,
är separabelt, - testmängdfamiljen är
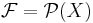 och
och - testmåttet
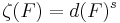 för
för 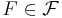
så är 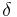 -Carathéodoryinnehållet det s-dimensionella
-Carathéodoryinnehållet det s-dimensionella 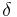 -Hausdorffinnehållet
-Hausdorffinnehållet
och yttre Carathéodorymåttet det s-dimensionella yttre Hausdorffmåttet
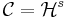 .
.
Yttre Lebesguemått
- Huvudartikel: Lebesguemått.
Andra exempel är det n-dimensionella yttre Lebesguemåttet som är 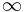 -Carathéodoryinnehållet i
-Carathéodoryinnehållet i  . Vi konstruerar det så att alla n-intervall är testmängder och testmåttet är det geometriska måttet för n-intervall.
. Vi konstruerar det så att alla n-intervall är testmängder och testmåttet är det geometriska måttet för n-intervall.
Mer precist, om 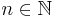 och
och
- metriska rummet
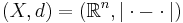 ,
, - testmängdfamiljen är
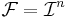 (familjen av alla n-intervall) och
(familjen av alla n-intervall) och - testmåttet är geometriska måttet
 för
för 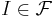
så är 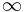 -Carathéodoryinnehållet det n-dimensionella yttre Lebesguemåttet
-Carathéodoryinnehållet det n-dimensionella yttre Lebesguemåttet
Yttre Favardmått
- Huvudartikel: Favardmått.
Ett speciellt exempel för Carathéodorys konstruktion är att man kan konstruera Favardmåttet i  med det. Vi konstruerar det så att alla Borelmängder är testmängder och testmåttet är en speciellt integralen definierad med hjälp av Grassmannmåttet.
med det. Vi konstruerar det så att alla Borelmängder är testmängder och testmåttet är en speciellt integralen definierad med hjälp av Grassmannmåttet.
Mer precist, om 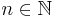 ,
, 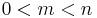 ,
, ![t \in [0,\infty]\,](/w/images/sv.rilpedia.org/math/6/0/3/6035be82f80bb854950d736b348c8dfc.png) och
och
- metriska rummet
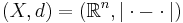 ,
, - testmängdfamiljen är
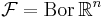 och
och - testmåttet för
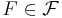 är:
är:
där
- mängden
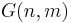 är Grassmannmångfalden,
är Grassmannmångfalden,
- måttet
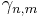 är Grassmannmåttet,
är Grassmannmåttet,
- funktionen
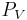 är ortogonal projektionen över delrummet
är ortogonal projektionen över delrummet 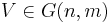 och
och
- operatoren
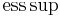 är väsentligt supremum med avseende på Grassmannmåttet
är väsentligt supremum med avseende på Grassmannmåttet 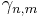 .
.
Då är yttre Carathéodorymåttet det m-dimensionella yttre Favardmåttet med konstanten 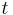 :
:
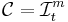 .
.
Se även
Referenser
- A. N. Kolmogorov & S. V. Fomin, Introductory Real Analysis, Dover, New York, 1970 ISBN 0-486-61226-0