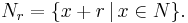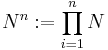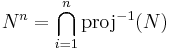Konstruktion av en icke mätbar mängd

Från Rilpedia

Version från den 10 april 2009 kl. 10.47 av Petter Strandmark (Diskussion)

(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Denna artikel utgör en fördjupning av artikeln om mätbarhet.

Inom det matematiska området måtteori kan det visas att det finns mängder som inte kan tilldelas ett n-dimensionellt Lebesguemått $m$ på ett rimligt sätt. Dessa mängder saknar längd, area eller volym.

Denna artikel skall nu visa att ett sådant mått inte finns genom att konstruera en speciell mängd och härleda en motsägelse.

Konstruktion

Vi skall konstruera en icke mätbar delmängd av 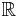$\R\,$ .

Vi börjar med att definiera en ekvivalensrelation genom att 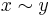$x\sim y \,$ om och endast om 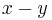$x - y\,$ är ett rationellt tal.

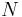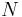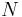Låt $N\,$ vara en mängd som innehåller exakt ett element från varje ekvivalensklass. Urvalsaxiomet garanterar att vi kan konstruera $N\,$ på detta sätt. Vidare kan vi anta att $N \subset [0,1]$ . Vi skall visa att $N\,$ inte kan vara mätbar.

Låt för alla rationella tal 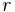$r\,$

$N_r = \{x + r \,|\, x \in N\}.$

Det vill säga: 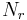$N_r\,$ är alla element i 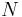$N\,$ förflyttade en sträcka 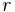$r\,$ . Nu gör vi följande observationer:

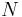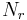$N\,$ och $N_r\,$ är translationer av varandra, så 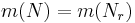$m(N) = m(N_r)\,$ eftersom Lebesguemåttet är Haarmåttet,
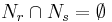$N_r\cap N_s = \emptyset$ då r och s är olika rationella tal.
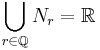
$\bigcup_{r\in \Q \cap [0,1]}N_r \subset [0,2]$ och $\bigcup_{r\in \Q}N_r = \R$

Eftersom $\Q \cap [0,1]$ är uppräknelig och Lebesguemåttet är sigma-additiv har vi

$\sum_{r\in \Q\cap [0,1]}m (N) = \sum_{r\in \Q\cap [0,1]}m(N_r) = m \left( \bigcup_{r\in \Q\cap [0,1]}N_r \right) \leq m ([0,2]) = 2$ .

Eftersom summan inte är ändlig måste 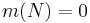$m (N)=0\,$ . Därför

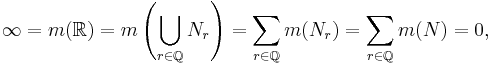
$\infty = m (\R) = m \left( \bigcup_{r\in \Q} N_r \right) = \sum_{r\in \Q}m(N_r) = \sum_{r\in \Q}m (N) = 0 ,$

vilket är en motsägelse. Därför N är icke Lebesguemätbar.

Nu vi vill konstruera icke mätbar mängd i $\R^n$ .

Låt

$N^n := \prod_{i=1}^n N$

var N är icke mätbar i 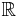$\R$ .

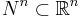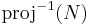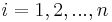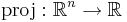Nu $N^n \subset \R^n$ . Eftersom projektionen är kontinuerlig funktion det är mätbar funktion. Därför $\mbox{proj}^{-1} (N)\,$ är icke mätbar för alla $i = 1,2,...,n\,$ var $\mbox{proj} : \R^n \rightarrow \R$ är en projektion.

Dessutom

$N^n = \bigcap_{i=1}^n \mbox{proj}^{-1} (N)\,$

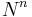så är $N^n\,$ icke mätbar eftersom mätbara mängder är en sigma-algebra.

Anmärkning

Måttet $m$ antogs vara uppräkneligt (till skillnad från ändligt) additivt. Detta antagande behövs i 1 och 2 dimensioner. För 3 och flera dimensioner behöver inte $m$ vara uppräkneligt additiv för att icke mätbara mängder skall existera. Detta visas till exempel av Banach-Tarskis paradox

Se även

Mått (matematik)

Måtteori

Mått (matematik); Konstruktion av en icke mätbar mängd
Definition: Yttre mått; Egenskaper hos mått
Begrepp: Nollmängd; Nästan överallt; Fullständigt mått
Integration: Mätbar funktion; Lebesgueintegration; Egenskaper hos måttintegral

Konstruktion av en icke mätbar mängd

Från Rilpedia

Innehåll

Konstruktion

Anmärkning

Se även

Måtteori

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda