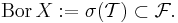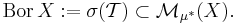Borelmått

Från Rilpedia

Version från den 10 april 2009 kl. 22.52 av Novn (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Ett Borelmått är inom matematik ett mått så att alla Borelmängder är mätbara, uppkallat efter franske matematikern Émile Borel.

Innehåll

Formell definition

Låt 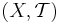(X,\mathcal{T})\, vara ett topologiskt rum och 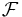\mathcal{F}\, en sigma-algebra i X. Då är ett mått

\mu : \mathcal{F} \rightarrow [0,\infty]

Borel om alla Borelmängder är mätbara. Mer precist,

\mbox{Bor}\,X := \sigma(\mathcal{T}) \subset \mathcal{F}.

Borel yttre mått

Låt 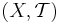(X,\mathcal{T})\, vara ett topologiskt rum, då ett yttre mått 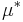\mu^*\, är Borel om alla Borelmängder är 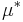\mu^*\,-mätbara:

\mbox{Bor}\,X := \sigma(\mathcal{T}) \subset \mathcal{M}_{\mu^*}(X).

Om X är ett metriskt rum så är ett yttre mått Borel om och endast om det är metriskt yttre mått.

Konstruktion för vissa Borel yttre mått

Huvudartikel: Carathéodorys konstruktion.

I ett metriskt rum kan man alltid konstruera ett naturligt Borel yttre mått med hjälp av den metriska strukturen. Den här konstruktionen är viktig eftersom vi kan konstruera den i alla metriska rum.

Exempel

Lebesguemåttet, Yttre Lebesguemåttet, Hausdorffmåttet och Yttre Hausdorfmåttet är Borel.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Borelm%C3%A5tt"
Personliga verktyg