Vattenpotential

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Vattenpotential är vattnets energinivå i en godtycklig punkt. Det är skillnaden i vattenpotential mellan två punkter i ett vattensystem, som får vattnet att förflyttas från punkten med högre vattenpotential till punkten med lägre vattenpotential. Om den totala vattenpotentialen är konstant inom hela vattensystemet, så sker ingen vattenrörelse.

Vattenpotentialgradienten, d.v.s. skillnaden i vattenpotential mellan två punkter i ett vattensystem dividerat med avståndet mellan dessa två punkter, bestämmer tillsammans med markens vattengenomsläpplighet hur snabbt vattnet strömmar i marken (Darcys lag).


Innehåll

Vattenpotentialens olika delar

Den totala vattenpotential (ψtotal) är summan av vattnets lägespotential (ψg), vattnets tryckpotential (ψT), vattnets osmotiska potential (ψo) och vattnets hastighetspotential (ψv).

Ψtotal = Ψg + ΨT + Ψo + Ψv


Lägespotential

Lägespotential (ψg) är vattnets lägesenergi i en punkt relativt en godtycklig referensnivå. Ofta väljs markytan eller ett täckdikesrör som referensnivå.

Tryckpotential

Tryckpotential (ψT) är vattnets tryckenergi i en punkt. Vattnets tryckpotential är positiv (större än 0) under grundvattenytan och negativ ovanför grundvattenytan. Vid negativ tryckpotential används ofta uttrycket tension eller kapillär potential.

Den permanenta vissningsgränsen brukar ligga på -150 meter vattenpelare, vilket motsvarar 98,9 % relativ luftfuktighet hos en +25-gradig luft.

Osmotisk potential

Osmotisk potential (ψo) förekommer bara i samband med osmos, som alltid kräver ett semipermeabelt membran, t.ex. växtrötternas cellmembran. Inom markvetenskapen och agrohydrologin är osmotisk potential intressant vid höga salthalter i marken och bevattning med salthaltigt vatten i ökenområden.

Hastighetspotential

Hastighetspotential (ψv) är vattnets rörelseenergi i en punkt. Hastighetspotentialen kan lätt försummas så fort det gäller grundvattnet och markvattnet. Vattnets hastighet brukar här bara bli några få centimetrar per dygn. Däremot måste vattnets hastighetspotential noga beaktas vid all rörströmning och kanalströmning, (se t.ex. Bernoullis ekvation).


Olika uttryckssätt för vattenpotential

Vattenpotentialen kan uttryckas på åtminstone tre olika sätt:

Energi per enhet massa

Detta är kanske det mest grundläggande uttrycket för vattenpotential. SI-enheten blir då 1 J/kg = 1 Nm/s2 = 1 m2/s2. Detta uttryckssätt är dock sällsynt bland praktikerna.

Energi per enhet volym

Då vatten i praktiken är en inkompressibel fluid, blir densiteten i det närmaste helt oberoende av tryckpotentialen. Så vattenpotentialen kan även uttryckas i energi per enhet volym. SI-enheten blir då 1 J/m3 = 1 Nm/m3 = 1 N/m2 = 1 Pa.

Vattenpotentialen kan alltså uttryckas i enheter för hydrostatiskt tryck, vilket ofta används för att uttrycka tryckpotential och osmotisk potential. Däremot används sällan hydrostatiskt tryck för att uttrycka lägespotential och hastighetspotential.

Energi per enhet tyngd (höjd vätskepelare)

Allt som kan uttryckas i en tryckenhet, kan också uttryckas i motsvarande höjd vätskepelare. 1 atmosfär = 10,33 meter vattenpelare = 760 mmHg.

Detta uttryckssätt underlättar starkt den praktiska hanteringen av vattenpotentialen. Om ett glas fylls med ett exakt 10 cm tjockt lager vatten (som hunnit ställa sig i jämvikt), är lägespotentialen vid vattenytan 10 centimeter vattenpelare och tryckpotentialen är 0. Vid glasets botten är är lägespotentialen 0 och tryckpotentialen = 10 centimeter vattenpelare. Mittemellan botten och vattenytan är både lägespotentialen och tryckpotentialen 5 centimeter vattenpelare.

När vattenpotentialen uttrycks som höjd vattenpelare, är meter vattenpelare, centimeter vattenpelare och millimeter vattenpelare vanliga enheter. Vid stora negativa undertryck (tension), används ibland även enheten pF.

När vattenpotentialen uttrycks i energi per tyngdenhet, brukar symbolen ψ bytas ut mot H (efter engelskans head i uttrycken hydraulic head, pressure head och metric head). På svenska brukar H översättas till vattenpelarens höjd.

Htotal = Hg + Hp + Ho + Hv

Matematisk sammanfattning av de olika uttrycken för vattenpotential

Nedanstående uttryck för lägespotential, tryckpotential och hastighetspotential ligger till grund för Bernoullis ekvation.

Energi

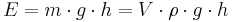E = m \cdot g \cdot h = V \cdot \rho \cdot g \cdot h Lägesenergi (J)
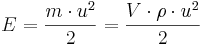E = \dfrac {m \cdot u^2}{2} = \dfrac {V \cdot \rho \cdot u^2}{2} Rörelseenergi (J)
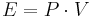E = P \cdot V Tryckenergi (J)
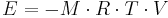E = -M \cdot R \cdot T \cdot V Osmotisk energi (J)

där

E = Energi (J)

m = Massa (kg)

g = Tyngdacceleration (ca 9,82 m/s2)

h = Höjd (m)

V = Volym (m3)

ρ = Densitet (ca 1000 kg/m3)

u = Hastighet (m/s)

P = Tryck (N/m2)

M = koncentration (mol/m3)

R = allmänna gaskonstanten (ca 8,3145 J/(mol K)

T = temperatur (K)


Energi per enhet massa

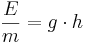\dfrac {E}{m} = g \cdot h Lägespotential (J/kg = m2/s2)
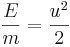\dfrac {E}{m} = \frac {u^2}{2} Hastighetspotential (J/kg = m2/s2)
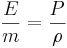\dfrac {E}{m} = \dfrac {P}{\rho} Tryckpotential (J/kg = m2/s2}
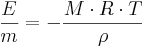\dfrac {E}{m} = - \dfrac {M \cdot R \cdot T} {\rho} Osmotisk potential (J/kg = m2/s2}


Energi per enhet volym

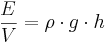\dfrac {E}{V} = \rho \cdot g \cdot h Lägespotential (J/m3 = Pa)
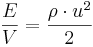\dfrac {E}{V} = \dfrac {\rho \cdot u^2}{2} Hastighetspotential (J/m3 = Pa)
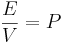\dfrac {E}{V} = P Tryckpotential (J/m3 = Pa)
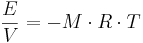\dfrac {E}{V} = -M \cdot R \cdot T Osmotisk potential (J/m3 = Pa)

Energi per enhet tyngd (höjd vätskepelare)

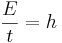\dfrac {E}{t} = h Lägespotential (meter vattenpelare)
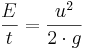\dfrac {E}{t} = \dfrac {u^2}{2 \cdot g} Hastighetspotential (meter vattenpelare)
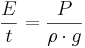\dfrac {E}{t} = \dfrac {P}{\rho \cdot g} Tryckpotential (meter vattenpelare)
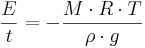\dfrac {E}{t} = - \dfrac {M \cdot R \cdot T}{\rho \cdot g} Osmotisk potential (meter vattenpelare)

där t = Tyngd (N)

Några exempel på praktisk tillämpning

Det finns flera tillfällen, då det är värdefullt att känna till storleken på en eller flera delkomponenter i den totala vattenpotentialen.


Flödesdimensionering

Nästan all flödesdimensionering kräver en detaljerad kunskap om vattnets lägespotential, tryckpotential och hastighetspotential. Dock är den osmotiska potentialen helt ointressant i dessa sammanhang. Se vidare under kanalströmning och rörströmning.


Vattnet i marken

För att kunna bedöma hur vattnet flödar i marken, är tryckpotentialen och lägespotentialen av primärt intresse. Vid riktigt småskaliga studier på lerjord, kan även den osmotiska potentialen vara intressant. Markvattnets hastighet är dock så låg, att hastighetspotentialen lätt kan försummas i dessa sammanhang.

Vid konstruktion av en pF-kurva, är kunskap om hur vattenhalten varierar med olika tryckpotential en absolut nödvändighet.

För att bedöma bevattningsbehovet, är tryckpotentialen absolut nödvändig. På salthaltiga jordar måste man dessutom känna till den osmotiska potentialen. Används salthaltigt bevattningsvatten, fordras dessutom kännedom om bevattningsvattnets osmotiska potential (för att kunna avgöra hur mycket överbevattning som behövs för att förhindra en försaltning av markytan).

För att kunna bedöma (den verkliga) transpirationens storlek, fodras kännedom om markens tryckpotential och osmotiska potential. Lägespotentialen kan som regel försummas i sammanhanget (liksom hastighetspotentialen).


Se även


Källor

Hillel D. 1980 Intoduction to Soil Physics. 364 pp. Academic Press Inc. ISBN 0-12-348520-0

Koorevar P, Melelik G och Dirksen C, 1983. Elements of Soil Physics, Developments in Soil Science 13, 230 pp. ISBN 0-444-42242-0

Hämtad från "https://sv.rilpedia.org/wiki/Vattenpotential"
Personliga verktyg