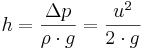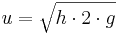Bernoullis ekvation

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Schematisk bild en förändring av tryck, temperatur, avstånd och hastighetsförändring över en rörvidgning

Tryck och hastighet i en stationär, inkompressibel och friktionsfri strömning längs en strömlinje kan uttryckas enligt följande ekvation under förutsättning att inget värme tillförs fluiden eller axelarbete uträttas:

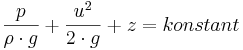
\dfrac{p}{\rho\cdot g} + \frac{u^2}{2\cdot g} + z = konstant

Enheten för termerna i ekvationen är (m);

p = statiska trycket i enhet (N/m2)

ρ = fluidens densitet i enhet (kg/m3)

g = tyngdaccelerationen i enhet (m/s2)

u = strömningshastigheten i enhet (m/s)

z = höjden över ett horisontalplan som angetts som referensplan i enhet (m).

Ekvationen är känd som Bernoullis ekvation och togs fram av den schweiziske matematikern Daniel Bernoulli som publicerade en av de första böckerna om strömmande fluider år 1738. Ekvationen ovan utvecklades dock ett par år senare.

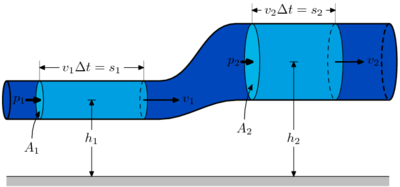
Betraktas en strömningslinje mellan 2 punkter med olika höjd över ett horisontellt referensplan erhålls vid förlustfri strömning;

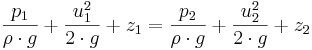
\dfrac{p_1}{\rho\cdot g} + \frac{u_1^2}{2\cdot g} + z_1 = \frac{p_2}{\rho\cdot g} + \frac{u_2^2}{2\cdot g} + z_2

Med ekvationen kan man bestämma strömningshastigheten och trycket i varje punkt längs en strömningslinje. Om även strömningsförlusterna mellan punkter 1 och 2 inkluderas utvidgas ekvationen till följande uttryck;

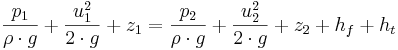
\dfrac{p_1}{\rho\cdot g} + \frac{u_1^2}{2\cdot g} + z_1 = \frac{p_2}{\rho\cdot g} + \frac{u_2^2}{2\cdot g} + z_2 + h_f + h_t

Den näst sista termen hf är strömningsförlusterna som uppstår p.g.a. fluidens viskositet, uttryckt som en höjdförlust i (m). Vid rörströmning tillkommer dessutom tilläggsförluster, ht.

Statiskt, dynamiskt tryck och totalt tryck:

Termen 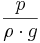\dfrac{p}{\rho\cdot g} utgör fluidens statiska tryck (tryckpotential).

Termen 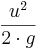\dfrac{u^2}{2\cdot g} utgör fluidens dynamiska tryck (hastighetspotential).

Summan av dessa blir fluidens totala tryck eller 'stagnationstryck' (total potential).


Innehåll

Praktiska tillämpningar

Pitotrör för bestämning av hastigheten för en strömmande fluid

Bernoullis ekvationen ligger till grund för en mängd tekniska tillämpningar inom strömningsmekaniken, alltifrån beräkning av hur mycket energi som kan utvinnas ur ett vattenkraftverk med en viss nivåskillnad mellan vattennivå i vattendammen och turbinhjulets placering till så enkla applikationer som exempelvis Pitot-röret, uppkallat efter Henri Pitot som uppfann en enkel metod för att mäta strömningshastigheten i floden Seine i Paris.


Pitot-röret

Höjden h, som vätskepelaren i ett pitot-rör stiger över den fria ytan, är ett uttryck för fluidens totala tryck, eftersom hastigheten i pitot-röret är noll.

h = \dfrac {\Delta p}{\rho \cdot g} = \dfrac {u^2}{2 \cdot g}

Genom att mäta höjden h kunde strömningshastigheten i floden bestämmas.

Omvänt kan pitotröret användas för att bestämma en farkosts hastighet relativt en stillastående fluid, för ett flygplan i luften eller för en båt i vattnet, genom att koppla en tryckmätare till röret:

u = \sqrt{h\cdot 2\cdot g}


Se även


Källor

  • Mechanics of Fluids , B.S. Massey, London
Hämtad från "https://sv.rilpedia.org/wiki/Bernoullis_ekvation"
Personliga verktyg