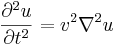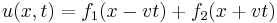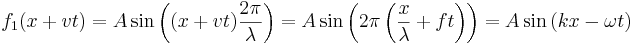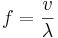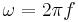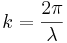Vågrörelse

Från Rilpedia

(Omdirigerad från Triangelvåg)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

För andra betydelser av "våg" se Våg

Vågor i vatten.

En våg eller vågrörelse är ett fysikaliskt fenomen som beskriver hur en störning av ett medium eller ett fält utbreder sig.

Vattenvågor är åskådliga exempel på vågutbredning när man kastar i en sten. Det är svårare att hitta åskådliga exempel med fält, eftersom de i allmänhet är osynliga. Om radiovågor inte utbredde sig med 300 miljoner m/s utan tagit det riktigt lugnt, kunde man ha ställt upp en mängd kompasser lodrätt på olika platser framför en radiosändare. Då kunde man ha sett att alla nordpilarna på ett visst avstånd från sändaren pekade uppåt, medan alla på ett lite större avstånd pekade neråt, och att detta skiftade rytmiskt med tiden. Det hade visat att sändarens elektromagnetiska fält utbreder sig vågformigt, och avslöjat både våglängden och utbredningshastigheten.

Vågor kan i allmänhet beskrivas matematiskt med vågekvationen som är en partiell differentialekvation. Utan extra randvillkor är lösningarna till denna så generella att den kan uppfyllas av en stor klass funktioner.

Kvantmekaniska partiklars fördelningssannolikhet beskrivas med hjälp av vågfunktioner. För att i detta fall beräkna hur vågfunktionen beter sig används Schrödingerekvationen.

Ett ljudvågsfenomen är svävning.

Innehåll

Vågegenskaper

Periodiska vågor kännetecknas av sina faser som beskriver toppar och dalar.

Vågor kan vara transversella, longitudinella, av blandad karaktär eller något annat.

  • Transversella vågor orsakar en störning som är vinkelrät mot vågens fortplantningsriktning. Ett exempel på detta är vågor på en sträng. I ett rep som spänts upp horisontellt mellan två fasta punkter som utsätts för en störning i vertikal led, rör sig repets enskilda partiklar i huvudsak enbart i vertikal led, oscillerande upp och ner, vinkelrätt mot vågens utbredningsriktning.
  • Longitudinella vågor orsakar en störning i samma riktning som de fortplantas. Ett exempel på detta är ljudvågor.
  • Blandade; ett exempel på detta är vattenvågor: vågen utbreder sig i en viss riktning, medan de enskilda vattenpartiklarna flyttas i en cirkulär bana som leder till en ändring i våghöjd.
  • Annat - kvantmekaniska vågfunktioner kan inte beskrivas som en utvikelse med en riktning.

Alla vågor har ett gemensamt beteende under vissa betingelser. Alla vågor kan erfara följande:

  • Reflexion - riktningsändring då vågen träffar en reflexiv gränsyta mellan två olika media.
  • Refraktion - riktningsändring då vågen träder in i ett nytt medium.
  • Diffraktion - spridning av vågor då de går igenom ett förhållandevis litet hål i en annars ogenomtränglig vägg.
  • Interferens - samverkan mellan två vågor som kommer i kontakt med varandra.
  • Dispersion - vågor som splittras upp efter frekvens.

Vågtyper

Man skiljer mellan olika typer av vågor:

Matematisk beskrivning

Vågor beskrivs av vågekvationen. För en våg i ett isotropt medium tar den formen

\frac{\partial^2 u}{\partial t^2}=v^2 \nabla^2 u

där v är vågens hastighet och 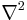\nabla^2 är laplaceoperatorn. I en dimension har denna ekvation lösningen

u(x,t)=f_1(x-vt)+f_2(x+vt)\,

där f1 och f2 är godtyckliga, två gånger kontinuerligt deriverbara funktioner. f1 beskriver en våg som färdas i den positiva riktningen längs x-axeln och f2 en som färdas i negativ.

En vågs amplitud är ett mått på den maximala störning som sker i mediet.

Periodiska vågor

Periodiska vågor kan beskrivas med hjälp av trigonometriska funktioner. Om 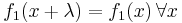f_1(x+\lambda)=f_1(x)\, \forall x kallas λ vågens våglängd och man kan skriva

f_1(x+vt)=A \sin\left((x+vt)\frac{2\pi}{\lambda}\right)=A \sin\left(2\pi \left(\frac{x}{\lambda} +ft\right)\right)=A \sin\left(kx-\omega t\right)

där A är vågens amplitud, f är dess frekvens, k dess vågtal och ω dess vinkelfrekvens. Dessa storheter förhåller sig till varandra som

f=\frac{v}{\lambda}
\omega= 2\pi f\,
k=\frac{2 \pi}{\lambda}

För allmänna vågor gäller att ω = ω(k), och då kallas 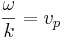\frac{\omega}{k}=v_p vågens fashastighet och 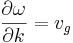\frac{\partial \omega}{\partial k}=v_g dess grupphastighet. Vågen överför information med grupphastigheten, och denna kan enligt speciella relativitetsteorin ej överstiga ljushastigheten i vakuum, 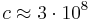c\approx 3\cdot 10^8 m/s. Fashastigheten överför ingen information, och kan därmed överstiga denna gräns.

Förhållandet ω = ω(k) kallas mediats dispersionsrelation. Om ω = vk kallas mediet dispersionsfritt och vp = vg (detta gäller till exempel i vakuum). Om detta inte gäller kommer en våg sammansatt av flera olika frekvenser att distorderas när den färdas i mediet, vilket kallas dispersion.

Vågformer

Benämningar på det grafiska utseendet hos periodiska signaler.

Sinusvåg
Fyrkantsvåg
Sågtandsvåg
Triangelvåg

Se även

Källor

  • Hecht, Eugene: Optics, Addison Wesley, San Francisco 2002, Fourth edition. ISBN 0-321-18878-0. 
Hämtad från "https://sv.rilpedia.org/wiki/V%C3%A5gr%C3%B6relse#V.C3.A5gformer"
Personliga verktyg