Vågekvation

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

En vågekvation är en partiell differentialekvation som beskriver beteendet hos olika typer av vågor, som exempelvis ljudvågor, ljusvågor och vattenvågor.

I en dimension är den homogena vågekvationen:

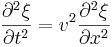
\frac{\partial^2 \xi}{\partial t^2} = v^2 \frac{\partial^2 \xi}{\partial x^2}

Den generella lösningen till denna ekvation ger 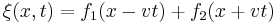\xi(x,t)=f_1(x-vt)+f_2(x+vt)\, vilket generellt sett kan beskriva alla endimensionella vågor. f1 beskriver en i högra riktningen gående våg med hastighet v, medan f2 beskriver en vänstergående våg med samma hastighet.

Se även



Stylised Lithium Atom.svg Denna artikel om fysik är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/V%C3%A5gekvation"
Personliga verktyg