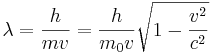Från Rilpedia

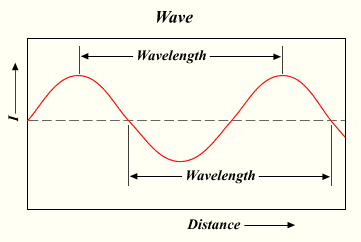
Våglängden är avståndet mellan repeterande delar av ett vågmönster. Den betecknas ofta med den grekiska bokstaven lambda (λ).

I en sinusvåg är våglängden avståndet mellan två motsvarande punkter i vågen, till exempel två toppar eller två dalar:

x-axeln representerar avstånd, och I någon varierande kvantitet (exempelvis lufttryck för en ljudvåg eller styrkan på ett elektriskt fält eller magnetfält för ljus), vid en given position i tid som funktion av x.

Våglängd har en omvänd relation till frekvens, antalet vågtoppar som passerar en punkt inom en given tid. Vågländen är lika med vågens hastighet delad med vågens frekvens. När det gäller elektromagnetisk strålning i vakuum, så är det ljusets hastighet c, så omvandlingen blir,

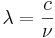(1)

där:

• λ = en elektromagnetisk vågs våglängd
• c = ljusets hastighet = 2,99792458·10⁸ m/s
• ν = vågfrekvens

För radiovågor är denna relation lätthanterad med denna formel: våglängden i meter = 300/frekvens i megahertz (MHz)

Louis-Victor de Broglie upptäckte att alla partiklar med rörelsemängd har en våglängd kallad de Broglievåglängd. För en relativistisk partikel ges denna våglängd av

där h är Plancks konstant, m₀ är partikelns vilomassa, och v är partikelns hastighet.

Många typer av vågmönster innehåller en blandning av sinusoidala vågor och språngvisa förändringar. Ett exempel är vägojämnheter, vilka kan inkludera kraftiga gupp.

Se även

• Vågrörelser på en vattenyta utgör en delvis transversell vågrörelse och följer i princip samma lagar som uttrycket (1) ovan. Se vidare vattenvågor.