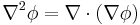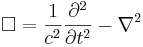Laplaceoperatorn

Från Rilpedia

(Omdirigerad från Laplaceoperator)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Laplaceoperatorn eller Laplaces operator är inom vektoranalysen en differentialoperator. Den har fått sitt namn efter Pierre Simon de Laplace. Laplaceoperatorn är lika med summan av alla andra ordningens partiella derivator av en beroende variabel. Laplaceoperatorn är en elliptisk operator med många applikationer inom fysiken och matematiken.

Detta motsvarar div(grad φ), därav användandet av symbolen nabla för att representera den:

$\nabla^2 \phi = \nabla \cdot ( \nabla \phi )$

Samt för vektorfält: 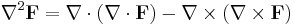$\nabla^2 \mathbf{F} = \nabla \cdot (\nabla \cdot \mathbf{F}) - \nabla \times (\nabla \times \mathbf{F})$

Den skrivs även som Δ.

Operatorn förekommer, till exempel, i Laplaces ekvation.

Koordinatrepresentation i 3 dimensioner

Laplaces operator är i kartesiska koordinater

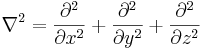$\nabla^2=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}$ ,

i cylindriska koordinater

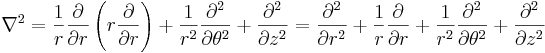$\nabla^2=\frac{1}{r}\frac{\partial}{\partial r}\left( r\frac{\partial}{\partial r}\right) +\frac{1}{r^2}\frac{\partial^2}{\partial \theta ^2}+\frac{\partial^2}{\partial z^2} =\frac{\partial^2}{\partial r^2} +\frac{1}{r}\frac{\partial}{\partial r}+ \frac{1}{r^2}\frac{\partial^2}{\partial \theta ^2}+\frac{\partial^2}{\partial z^2}$ ,

och i sfäriska koordinater

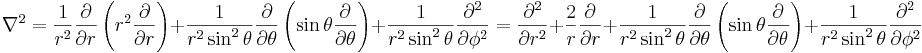$\nabla^2=\frac{1}{r^2}\frac{\partial}{\partial r}\left( r^2 \frac{\partial}{\partial r}\right) +\frac{1}{r^2\sin ^2 \theta}\frac{\partial}{\partial \theta}\left( \sin \theta \frac{\partial}{\partial \theta} \right)+\frac{1}{r^2\sin ^2 \theta}\frac{\partial^2}{\partial \phi^2}= \frac{\partial^2}{\partial r^2} +\frac{2}{r}\frac{\partial}{\partial r} +\frac{1}{r^2\sin ^2 \theta}\frac{\partial}{\partial \theta}\left( \sin \theta \frac{\partial}{\partial \theta} \right)+\frac{1}{r^2\sin ^2 \theta}\frac{\partial^2}{\partial \phi^2}$ .

d'Alemberts operator

En motsvarighet som ibland används inom relativitetsteori och i Minkowskis rumtid eller för att skriva ut vågekvationen betecknas $\Box$ och kallas d'Alemberts operator. I 3+1-dimensionella rum (3 rumsdimensioner och 1 tidsdimension) har den formen