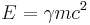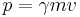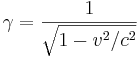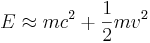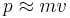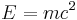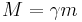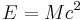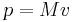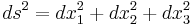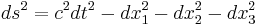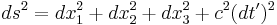Speciella relativitetsteorin

Från Rilpedia

(Omdirigerad från Speciell relativitetsteori)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Den speciella relativitetsteorin är en fysikalisk teori, publicerad 1905 av Albert Einstein och beskriver rummets och tidens egenskaper när man kan bortse från tyngdkraftens - gravitationens - inverkan. Den formel som den stora allmänheten förknippar med teorin är E = mc², där E är energi, m är massa och c² ljushastigheten i vakuum i kvadrat.

Einsteins speciella relativitetsteori kom att ersätta de föreställningar om rum och tid som finns i Newtons fysik samtidigt som den inlemmade elektromagnetismen så som den beskrivs av Maxwell enligt dennes elektromagnetiska ekvationer. Anledningen till att den kallas speciell (även kallad "särskild" i skolböcker) är inte att den är mer omfattande eller svårförståelig än den allmänna relativitetsteorin, som Einstein kom att lägga fram tio år senare, utan att den begränsar sig till att "endast" beskriva förhållanden där gravitationen kan lämnas utanför. I den allmänna relativitetsteorin som Einstein förevisade år 1915 utvidgade han teorin så att den kom att omfatta även gravitationen.

Innehåll

1 Bakgrund och motivering till den speciella relativitetsteorin
2 Den speciella relativitetsteorins status
3 Konsekvenser av speciella relativitetsteorin
4 Ljushastighetens konstans
5 Avsaknad av ett absolut referenssystem
6 Massa, rörelsemängd och energi
7 Samtidighet och kausalitet
8 Rumtidens geometri
9 Tester på speciella relativitetsteorins postulat
10 Enhetsanalys av E=mc² i SI-systemet
11 Exempel på tillämpningar
12 Referenser
- 12.1 Litteratur
13 Se även
14 Externa länkar

Enligt den speciella relativitetsteorin bildar rummet (med de tre dimensionerna längd, höjd och bredd) och tiden tillsammans ett fyrdimensionellt system, den så kallade rumtiden, och mätningar av tid och avstånd beror av observatörens rörelse. Det finns inga absoluta rörelser eller tidsförlopp utan dessa är relativa och ett föremåls hastighet kan bara anges i förhållande till andra föremål. Teorin anger också att det finns en högsta hastighet, nämligen ljusets hastighet i vakuum och att denna hastighet är konstant och lika för alla observatörer. De fysikaliska lagarna är desamma för alla observatörer. Föremål som rör sig i förhållande till observatören förkortas i rörelseriktningen (enligt observatörens mätningar i denna riktning, någon lokal kontraktion av objektet förekommer ej) och klockor i rörelse går långsammare än klockor i vila. Teorin anger också att massa är en form av energi.

E=mc²

Bakgrund och motivering till den speciella relativitetsteorin

Redan innan den speciella relativitetsteorin formulerades, hade bland annat Hendrik Lorentz och George Francis FitzGerald observerat att elektromagnetiska krafter varierar beroende på hur de observeras. Exempelvis beror det magnetiska fältet på observatörens rörelsetillstånd, en observatör i vila i förhållande till det elektromagnetska fältet uppfattar inget magnetiskt fält, endast en observatör i relativ rörelse kan registrera ett magnetiskt fält. FitzGerald och Lorentz föreslog oberoende av varandra (1892 resp. 1895) teorier innebärande att objekt som rör sig i förhållande till en stationär observatör genomgår en fysisk förkortning, så kallad längdkontraktion (Lorentzkontraktion eller Lorentz-FitzGerald-kontraktion). Lorentz inkorporerade i sin teori också idén att tiden gick långsammare, så kallad tidsdilatation, för det rörliga objektet och konstruerade formler som beskrev denna, den så kallade Lorentztransformationen. Han tänkte sig att universum genomsyrades av en osynlig eter och att rörelse genom detta medium påverkade kropparna. Dessa teorier tycktes lösa den konflikt mellan elektromagnetism och klassisk Newtonsk fysik som uppstått genom att Lorentz formler sammanföll med Newtons rörelselagar vid hastigheter som var små i förhållande till ljusets hastighet. Lorentz eter-teori blev dock kritiserad (även av honom själv) för sin delvis godtyckliga natur.

Även om det var Lorentz som först formulerade de grundläggande sambanden lyckades Einstein härleda dessa ur en mer grundläggande teori. Han utgick från att fysikens lagar borde vara lika - invarianta - för alla observatörer, och härledde bl.a Lorentztransformationen som en konsekvens.

Den speciella relativitetsteorin beskriver vanligtvis observatörer och kroppar som befinner sig i vila, eller rör sig med konstant hastighet, i förhållande till varandra. En vanlig missuppfattning är att teorin inte hanterar fall då rörelsen är accelererande. Den speciella relativitetsteorin kan dock på ett korrekt sätt beskriva hur accelererande kroppar beter sig i ett konstant gravitationsfält eller som rör sig i roterande referenssystem. Exempel på detta är tvillingparadoxen eller när en raket accelererar till höga hastigheter. Den kan inte beskriva rörelser i varierande gravitationsfält.

Den speciella relativitetsteorins status

Speciella relativitetsteorin är numera universellt accepterad av det vetenskapliga samfundet. Den är experimentellt mycket väl bekräftad^[1] och inga avvikelser från de resultat teorin förutsäger har observerats. Det har dock funnits och finns än i dag forskare som har föreslagit alternativ. En sådan alternativ teori är den dubbelt speciella relativitetsteorin, där inte bara ljusets hastighet är konstant utan även en viss (mycket liten) längd uppfattas lika av alla observatörer.

Konsekvenser av speciella relativitetsteorin

Speciella teorins postulat om konstant ljushastighet och avsaknad av absoluta referensramar har flera konsekvenser som rent intuitivt kan uppfattas som bisarra, exempelvis:

Tidsskillnaden mellan två händelser är inte något objektivt, utan beroende av de olika observatörernas relativa rörelse i förhållande till varandra.
Två händelser som tycks ske samtidigt (men på olika platser) ur en observatörs synpunkt, kan uppfattas ske vid olika tidpunkt, och i godtycklig ordning, av andra observatörer.
Ett föremåls storlek beror på en observatörs relativa hastighet.
Tvillingparadoxen, ett tankeexperiment där en tvilling beger sig ut på en rymdresa med höga hastigheter och finner vid återvändandet att den kvarvarande tvillingen har åldrats mer än resenären.

Förutom att speciella teorin förändrat vår föreställning om tid och rum tvingar den oss också att omvärdera begreppen massa, rörelsemängd och energi. Liksom den för samman de båda förstnämnda till begreppet rumtid, visar den att rörelsemängd och energi kan ses som olika aspekter på samma sak. Detta ger konsekvenser såsom:

En partikels massa ökar när dess hastighet ökar (den kinetiska energin ger ett tillskott till massan)

Ljushastighetens konstans

Den speciella relativitetsteorin postulerar att ljusets hastighet i vakuum är lika för alla observatörer i likformig relativ rörelse. Att ingen sådan observatör har "företräde" med avseende på någon annan, utan att fysikens lagar måste vara lika för alla observatörer, leder till fenomen som längdkontraktion och tidsdilatation enligt Lorentztransformationens formler.

Notera att ljusets hastighet i ett medium är lägre än i vakuum. I ett medium kan det även förekomma hastigheter större än ljusets, s k Čerenkov-ljus.

Avsaknad av ett absolut referenssystem

Den speciella relativitetsteorin avvisar föreställningen om att det existerar ett oberoende referenssystem för mätning av tid och rum. Istället anger den att alla system, där observatörer rör sig med konstant hastighet, inertialsystem, är likvärdiga och att därför fysikens lagar måste ge samma resultat för dem alla. Denna så kallade relativitetsprincip kan ses redan hos Galilei, och är en del av även den Newtonska fysiken. Men i slutet av 1800-talet förespråkades idén att universum är fylld av osynlig substans, den så kallade etern, genom vilken elekromagnetiska vågor fortplantade sig likt ljudvågor genom luften. Etern utgjorde ett absolut referenssystem mot vilket rörelse och hastigheter kunde mätas, och samtidigt som vågrörelser i den kunde växelverka med materia, antogs den inte bjuda något motstånd mot föremål som passerar genom den.

Olika tester som kulminerade med Michelson-Morleys experiment år 1887, visade att antingen stod jorden stilla, eller så måste föreställningen om etern och ett absolut referenssystem överges.

Massa, rörelsemängd och energi

Fil:Gamma.svg

Lorentzfaktorn

För att konserveringslagen om energins bevarande ska hålla vid höga hastigheter, krävs en förändring av formlerna för rörelseenergi och rörelsemängd som används i den klassiska fysiken. För ett föremål med massan m som rör sig med hastigheten v, ges dess totalenergi E och rörelsemängd p av

$\ E = \gamma m c^2$

respektive

$\ p = \gamma m v$

där Lorentzfaktorn γ

$\gamma = \frac{1}{\sqrt{1 - v^2/c^2}}$

och c är ljusets hastighet. Termen γ som ofta förekommer inom relativitetsteorin erhålls ur ekvationerna i Lorentztransformationen. Relationen mellan totalenergin och rörelsemängden ges av formeln

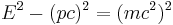$\ E^2 - (p c)^2 = (m c^2)^2$ .

Om hastigheten v är mycket liten i förhållande till c så fås genom en Taylorutveckling av formeln för γ att

$\ E \approx m c^2 + \frac{1}{2}m v^2$

och

$\ p \approx m v$

vilket överensstämmer med de klassiska formlerna.

Om man tar ett föremål i vila (v=0 och därmed γ=1) så ger ovanstående formel för energi inte värdet noll utan reduceras till den berömda formeln:

$\ E = m c^2$

Det vill säga även när ett föremål är i vila så återstår en viss mängd energi, den så kallade viloenergin. (Denna viloenergi ger ingen konflikt med den klassiska fysiken eftersom den är konstant. När det gäller rörelseenergi så är det skillnaden i energi som är av betydelse.)

Formeln visar att massa, ur relativistisk synvinkel, kan betraktas som en form av energi, och därför teoretiskt skulle kunna omvandlas till andra former, såsom värme och ljus. Att detta inte bara är teori demonstreras tydligt av de stora mängder energi som kan frigöras vid olika former av kärnreaktioner.

När v närmar sig c, så går nämnaren i formeln för γ mot noll, och därmed energin mot oändligheten. Det vill säga när ett föremåls hastighet närmar sig ljusets, så går den energimängd som krävs för att accelerera det ytterligare mot oändligheten, vilket gör det omöjligt att nå ljusets hastighet. Endast partiklar som saknar massa, såsom fotonen, kan i praktiken nå ljushastigheten. De kan heller inte gå långsammare, utan måste i alla referenssystem röra sig med denna hastighet. Namnet tachyon har används för en hypotetisk partikel som skulle röra sig fortare än ljusets hastighet, men hittills har existensen av sådana partiklar inte kunnat påvisas experimentellt.

Det sägs ofta att den speciella relativitetsteorin anger att ett föremåls massa ökar när hastigheten ökar. Emellertid används här två olika definitioner av begreppet massa. I formlerna ovan står m för föremålets vilomassa som förblir konstant och är lika i alla referenssystem. Ett annat begrepp är föremålets relativistiska massa - M som ges av

$\ M = \gamma m$

där γ är samma som i formlerna för energi och rörelsemängd. Eftersom γ ökar med hastigheten, gör också den relativistiska massan det. Om hastigheten är noll så är γ=1 och den relativistiska massan lika med vilomassan. Ibland är det praktiskt att skriva om de första formlerna som

$\ E = M c^2$

och

$\ p = M v$

Relativitetsteorin medför att det även finns en övre gräns med vilken påverkan av gravitationen kan röra sig - ljushastigheten i vakuum. Detta avviker från den klassiska teorin för gravitation så som den formulerades av Isaac Newton. Trots det är gravitationskraften mellan två kroppar alltid riktad mot kropparnas ögonblickliga position, inte en fördröjd position. Om gravitationen från solen var riktad mot solens position för åtta minuter sedan hade det tydligt märkts i observationerna.

Samtidighet och kausalitet

Detta avsnitt är en sammanfattning av Samtidighet

Ljuskon

Den speciella relativitetsteorin säger att händelser som tycks ske samtidigt i vissa referenssystem inte behöver göra det i andra system, utan kan där ske i godtycklig ordning. Detta kan tyckas upphäva de normala lagarna för orsak och verkan, vilket dock inte är fallet.

I bilden till höger är intervallet AB 'tids-lika', d.v.s det är hypotetiskt möjligt för materia att förflytta sig från A till B. Om händelsen A inträffar före B, så gör den det i alla referenssystem.

Intervallet AC i diagrammet är 'rum-lika', det vill säga det är inte möjligt för materia eller ljus (eller information) att förflytta sig från A till C. Eftersom ingenting kan överföras från A till C, så kan det inte finnas någon orsakspåverkan mellan dem. Dessutom kan händelsen A inträffa före C i vissa referenssystem, ske samtidigt i andra, och inträffa efter C i ytterligare andra.

Rumtidens geometri

Den speciella relativitetsteorin använder ett 'platt' 4-dimensionellt så kallat Minkowski-rum, normalt kallat rumtiden. Denna rymd är tämligen likt ett 3-dimensionellt Euklidiskt rum, vilket gör det relativt åskådligt.

Avståndsdifferentialen, ds, i ett 3-dimensionellt linjärt rum definieras som:

$ds^2=dx_1^2+dx_2^2+dx_3^2$

där $d x 1, d x 2$ och $d x 3$ är differentialerna i respektive dimension. I speciella relativitetens geometri läggs sedan tiden till som en fjärde dimension, som oftast tas som den nollte dimensionen. Ekvationen för avståndsdifferentialen i rumtiden är i Minkowskirummet

$ds^2=c^2dt^2 - dx_1^2 - dx_2^2 - dx_3^2$

där man ofta enligt konvention väljer att sätta minustecken framför rumskoordinaterna och plustecken framför tiden. Det omvända förekommer också, framförallt i den allmänna relativitetsteorin.

Ibland hanteras tidskoordinaten med hjälp av imaginära tal, och $t$ byts då ut mot $i t'$ , vilket, om konventionen för minustecken ändras, ger formeln:

$ds^2=dx_1^2+dx_2^2+dx_3^2+c^2(dt')^2$

Detta är dock numera mindre vanligt, och förekommer mycket sällan i teknisk litteratur.

För att lättare kunna åskådliggöra rumtiden i 3 dimensioner kan man ta bort en av rumsdimensionerna så att man har två rumsdimensioner och en tidsdimension:

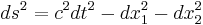$ds^2=c^2dt^2 - dx_1^2 - dx_2^2$ .

Ett föremål som rör sig med konstant hastighet genom rymden kan beskrivas som en rät linje genom rumtiden. Andra typer av rörelser ger andra typer av kurvor. En sådan kurva brukar kallas föremålets världslinje.

Ljusstrålar som anländer till eller utgår från en given punkt vid en given tid kan åskådliggöras med en dubbelkon kring punktens rumtid-koordinat - en så kallad ljuskon som beskrivs av ekvationen

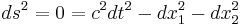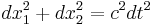
$ds^2=0=c^2dt^2 - dx_1^2 - dx_2^2$ eller $dx_1^2+dx_2^2=c^2dt^2$

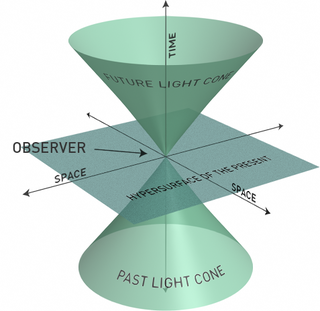
Ljuskon - (den 3-dimensionella) ytan av alla möjliga ljusstrålar som går till eller ifrån en punkt i rumtiden, här reducerat till 2 dimensioner.

Ofta brukar man anpassa enheterna så att ljuskonen bildar en 45-graders vinkel så som på bilden till höger.

Denna dubbelkon delar in rumtiden i tre områden.

Punkter i området innanför den övre konen representerar framtiden för den ursprungliga händelsen, och punkter innanför den undre konen representerar det förflutna. Kurvor som förbinder observatören (där båda konerna har sin spets) med punkter inom konerna kallas tidslika och representerar världslinjer för föremål som rör sig med hastigheter mindre än ljusets.
Punkter på konerna representerar nuet och utgörs av händelser som kan nås av ljusstrålar från den första händelsen. Världslinjer på denna yta kallas ljuslika och representerar ljusstrålar eller partiklar som hela tiden rör sig med ljusets hastighet. När vi vi observerar stjärnhimlen är det i princip denna del av rumstiden vi ser.
Punkter utanför konerna representerar händelser som inte är observerbara. Kurvor som förbinder den givna punkten med sådana punkter kallas rumslika och kan representera rums-dimensioner så som längd och bredd, snarare än vara världslinjer för ett föremål.

Tester på speciella relativitetsteorins postulat

Michelson–Morleys experiment - mätning av rörelse genom etern
Hamars experiment - mätning av motstånd mot eterflödet
Trouton-Nobles experiment - elektrostatisk påverkan orsakad av rörelse genom etern
Kennedy-Thorndikes experiment - test av Lorentz-Fitzgerald-kontraktion

Enhetsanalys av E=mc² i SI-systemet

I ekvationen E=mc² har vänsterledet i SI-systemet enheten Joule (J) och högerledet har enheten kg·(m/s)², där kg, m och s är grundenheter. J definieras som newtonmeter, Nm, och N är in sin tur definierat som kg·m/s². Slår vi ihop detta får alltså att

J = Nm = kg·a·m = kg·m/s²·m = kg·m²/s²

Högerledet faktoriserar sen som kg·(m/s)² = kg·(m/s)·(m/s) = kg·m²/s², så vänster- och högerleden har samma dimensioner.

Detta kan vara ett sätt att försöka förstå hur massa och energi kan anses vara ekvivalenta. Det är dock inte ett bevis för sambandet, det visar bara att mc² har samma enhet som E. Man kan jämföra med den traditionella formeln för rörelseenergi E=mv²/2.

Exempel på tillämpningar

Satellitnavigering

De atomur som används i satellitnavigeringssystem som exempelvis GPS påverkas både av effekter från den speciella och den allmänna relativitetsteorin, och tar också hänsyn till dessa.

Kosmisk strålning

Ett exempel på "klockor" som rör sig med hög hastighet relativt oss är de fenomen i form av sekundärstrålning som inträffar när kosmisk strålning träffar de övre skikten i jordens atmosfär. En del av sekundärstrålningens partiklar är instabila och sönderfaller med en bestämd halveringstid, det vill säga efter en viss tid är antalet kvarvarande partiklar reducerat till hälften. På grund av tidsdilatationen kommer partiklarna att tränga mycket längre ned i atmosfären än vad som motsvarar halveringstiderna mätta med jorden som referenssystem och möjliggör observationer av vissa partiklar vid jordytan vilka skulle vara praktiskt sett mycket svåra att observera om tidsdilatation ej förekom.

Addition av hastigheter

Vi tänker oss ett referenssystem A med punkterna X och Y. A observerar en observatör B som färdas mellan X och Y i likformig linjär rörelse, med hastigheten v. A observerar också C som färdas mellan Y och X i likformig linjär rörelse, med hastigheten v. A observerar också att B passerar X samtidigt som C passerar Y.

Enlig Newtons mekanik skulle B mäta Cs hastighet till 2v, vilket stämmer bra när v << c. Men det skulle innebära en hastighet större än c om v> c/2. Men enligt relativitetsteorin kommer B att mäta ett lägre värde på den relativa hastigheten. Om B till exempel mäter längden mellan X och Y kommer han enligt längkontraktionen uppfatta det som om avståndet är mindre än det är för A, och hastigheten (avståndet per tidsenhet) proportionsvis lägre.

Referenser

↑ Experimental basis of SR översikt av Tom Roberts (2007).

Litteratur

Taylor, E F, Wheeler J A Spacetime Physics. Introduction to Special Relativity, 1992

Se även

Personer:

Fysik och matematik:

Externa länkar

[0] Experimental basis of SR översikt av Tom Roberts (2007).

[1]