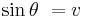Rumtid
Från Rilpedia
Rumtid är en sammanslagning av rummet och tiden till en enhet, där tiden bildar en extra fjärde dimension ihop med rummets tre vanliga dimensioner längd, bredd och höjd. En punkt i den fyrdimensionella rumtiden kallas en händelse.
Begreppet rumtid introducerades av den tyske matematikern Hermann Minkowski år 1908 som ett sätt att ge en geometrisk beskrivning av de förändringar av tid och rum som Albert Einstein formulerade i sin speciella relativitetsteori år 1905. Relativistiska fenomen som längdkontraktion och tidsdilatation kan beskrivas som att de koordinatsystem som beskriver olika "observatörers" uppfattning av omvärlden (deras "referenssystem") är roterade i förhållande till varandra i rumtiden. (Detta kräver dock en lite mer komplicerad representation av rumtiden än att bara lägga till tiden som en fjärde dimension - ett s.k. Minkowskirum.)
Med den allmänna relativitetsteorin utökades rumtidsbegreppet, så att den fyrdimensionella rumtiden kan ses som en "yta" i ett rum med fler dimensioner. Under frånvaro av massiva objekt och accelererande rörelse är denna "yta" plan och rätlinjig, men under påverkan av gravitationskrafter, eller vid accelererande rörelse, buktar denna yta i den nya dimensionens riktning och de tidigare räta koordinatlinjerna blir böjda geodetiska linjer i en "krökt" rumtid. En sådan extra dimension är egentligen bara ett sätt att åskådliggöra krökningen av rumtiden. Rent matematiskt brukar den allmänna relativitetsteorin beskriva rumtiden som ett fyrdimensionellt rum med icke-euklidiska egenskaper. Inom slingkvantgravitation kallar man samma begrepp för rumtidsväv.
Innehåll |
Visualisering av rumtiden i den speciella relativitetsteorin
Eftersom vi inte direkt kan uppfatta ett fyrdimensionellt rum brukar man ofta för enkelhets skull plocka bort en av rumsdimensionerna och visualisera rumtiden med bara 2 rumsdimensioner. Man brukar också sätta skalan på rumsdimensionerna så att ljushastigheten c blir = 1. Därigenom får exempelvis ett år på tidsaxeln samma längd som ett ljusår på rumsaxlarna.
- Händelser
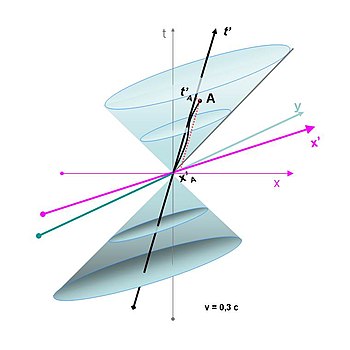
- En händelse på platsen med rumskordinaterna x och y vid tidpunkten t representras då av en punkt (x,y,t) i ett tredimensionellt koordinatsystem som i bilden till höger. Ett föremål (för enkelhets skull representerat som en enda punkt) som rör sig med konstant hastighet genom rummet kan beskrivas som en rät linje genom rumtiden. Linjens lutning är ett mått på hastigheten - ett stillastående föremål representeras av en lodrät linje, och ju fortare föremålet rör sig desto snedare lutar linjen. Andra typer av rörelser ger andra typer av kurvor. En sådan kurva, som på detta sätt visar föremålets position vid alla tidpunkter, kallas dess världslinje. Punkten A med koordinaterna (xA,0,tA) i bilden till höger visar en en sådan händelse och dess världslinje.
- Nuet
- Origo representerar händelsen "här och nu". Ljusstrålar som anländer eller utgår från denna händelse-punkt bildar två koner med spetsarna i origo. Med den vedertagna skalan bildar dessa ljuskoner 45° vinkel mot axlarna. Punkterna på ljuskonerna representerar fotoner som just nu anländer hit och sedan avlägsnar sig igen. Dessa fotoners världslinjer utgör räta linjer som går genom origo och ligger utefter ytan på konerna. Sådana världslinjer brukar därför kallas ljuslika, och punkterna på dem representerar nuet på så sätt, att när vi just nu observerar stjärnhimlen är det den delen av rumtiden vi ser.
- Framtiden och det förflutna
- Eftersom inget föremål enligt relativitetsteorin kan röra sig fortare än ljuset, måste världslinjen för ett föremål som befinner sig här och nu ligga innanför dessa koner. Punkter innanför den övre konen representerar föremålets tänkbara framtid, och de innanför den undre konen dess möjliga förflutna. Sådana kurvor som ligger innanför dessa koner, och alltså representerar världslinjer för föremål som rör sig med lägre hastighet än ljuset, kallas tidslika kurvor.
- "Annorstädes"
- Punkter som befinner sig utanför konerna representerar händelser som inte är en del av observatörens förflutna eller framtid, och som därför inte är tillgängliga för eller kan påverka denna. (Information om dessa händelser når dock observatören så småningom, när ljuskoner som utgår från dem slutligen överlappar den egna ljuskonen.) Kurvor som förbinder origo med sådan händelser kan inte utgöra verkliga världslinjer. De representerar snarare i vissa fall rumsdimensioner och kallas för rumslika.
- "Parallella realiteter"
- Förutom att bara tänka sig händelser som ligger inom respektive utanför en kon kan man tänka sig en mängd parallella koner där världslinjerna skiljer sig från varandra. Mängden händelser eller samlingen av utfall ses då som oändligt, men utfallsrummen är isolerade från varandra.
Rumtid och Lorentztransformation
Rumtiden åskådliggjord på ovanstående sätt är inte lika för alla utan beror på observatören och dennas rörelse. Enligt den speciella relativitetsteorin förändras tid och rum enligt Lorentztransformationens formler och ger upphov till tidsdilatation och längdkontraktion. Bilden till höger visar hur rumtiden förändras för en person som färdas med 30 % av ljusets hastighet i x-axelns riktning i förhållande till en annan person, sett ur den senares synvinkel. De plan som anger en viss tidpunkt för den person som rör sig (visade via cirklarna i ljuskonerna) lutar i förhållande till stillastående personens tidsplan, och den förras x-axel och tidsaxel är vridna mot varandra jämfört med den stillastående personens axlar. Dessutom är skalan på dessa axlar förändrad (vilket inte syns på bilden) så att tidsaxeln är utdragen och x-dimensionen är ihoptryckt i förhållande till den stillastående personen.
Sammanfattningsvis ger den hittills visade sättet att visa rumtiden, som ett enkelt euklidiskt rum med tiden som en extra dimension, ingen riktigt tillfredsställande bild av hur rumtiden egentligen beter sig. Istället brukar en mer abstrakt typ av matematiskt rum - ett s.k. Minkowski-rum - användas.
Avstånd i rumtiden - rumtidintervall
I ett traditionellt tredimensionellt euklidiskt rum definieras avståndet s mellan två punkter A =(xA,yA,zA) och B =(xB,yB,zB) som:  eller uttryckt på ett annat sätt
eller uttryckt på ett annat sätt 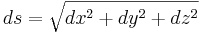
I ett fyrdimensionellt Minkowski-rum definieras istället för avståndet mellan två punkter i rummet det så kallade rumtidintervallet ds mellan två händelser i rumtiden som ds2 = dt2 − dx2 − dy2 − dz2. Minustecknen i de sista termerna medför att värdet kan bli både positivt och negativt. (Ett annat, ålderdomligt sätt att uttrycka detta är att istället för att använda tiden t som 4:e dimension så används det imaginära uttrycket it som enhet. Eftersom i2 = -1 får alla termerna då samma förtecken.
Några egenskaper för rumtidintervall:
- Händelser mellan vilka intervallet är positivt, ligger i varandras framtid eller förflutna (innanför ljuskonerna). Ett sådant intervall kallas tidslikt.
- Intervallets storlek är invariant och oberoende av vem som mäter det, och ett mått på den reella tidsdifferensen som uppmäts av en observatör som "färdas" mellan händelserna.
- Händelser som ligger på ytan av ljuskonerna har ett intervall som är lika med noll. För en foton som rör sig med ljusets hastighet från en viss händelsepunkt står tiden helt stilla, och i viss bemärkelse kan sägas "inte komma någonstans" utan alltid befinner sig på noll-avstånd från utgångspunkten. Ett sådant intervall kallas ljuslikt.
- Händelser som befinner sig "annorstädes", utanför ljuskonerna, har ett negativt rumtidintervall till utgångspunkten, vilket inte riktigt kan åskådliggöras i ett koordinatdiagram av ovanstående typ. Ett sådant intervall kallas rumslikt.
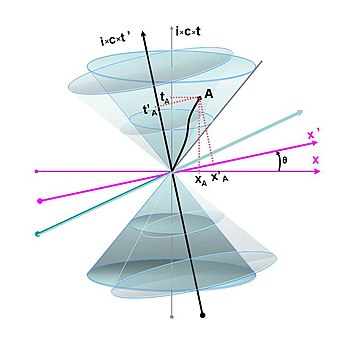
Transformation av referensramar i ett Minkowski-rum
Genom att använda ett Minkowski-rum istället för ett vanligt euklidiskt rum blir effekterna av Lorentztransformationen betydligt enklare att åskådliggöra. Istället för den förvrängning som syntes i förra bilden, kommer nu koordinatsystemet för en person som rör sig, att rotera i förhållande till en stillastående persons koordinatsystem. Ju större hastighet, desto större rotation. Det syns tydligt hur det som ena personen uppfattar som ren tid respektive ren rumsdimension, för den andra personen blir en blandning av rum och tid. Vinkeln θ för denna rotation ges av formeln: