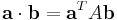Skalärprodukt
Från Rilpedia
Skalärprodukt inom vektoralgebran är en inre produkt, definierad på 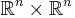 , en bilinjär funktion av två vektorer
, en bilinjär funktion av två vektorer 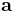 och
och 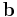 (eller
(eller 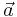 och
och 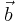 ) som definieras som produkten av beloppen (längderna) av vektorerna och vinkeln mellan dem, enligt
) som definieras som produkten av beloppen (längderna) av vektorerna och vinkeln mellan dem, enligt
där α är den minsta vinkeln mellan vektorerna. Om b har längden 1, kan detta tolkas som att skalärprodukten ger längden av a:s projektion på b.
Definitionen ger att om skalärprodukten mellan två nollskilda vektorer a och b är noll så måste 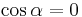 , dvs vektorerna a och b är vinkelräta mot varandra.
, dvs vektorerna a och b är vinkelräta mot varandra.
Om vi känner vektorernas komponenter i en ortonormerad bas, dvs 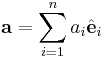 samt
samt 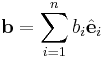 och
och 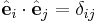 där δij är Kroneckerdeltat, så kan skalärprodukten även skrivas
där δij är Kroneckerdeltat, så kan skalärprodukten även skrivas
Mer generellt gäller att
där A är en inverterbar, postivt definit n×n-matris och 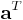 är transponatet av a, (a och b betraktas här som 1×n-matriser).
är transponatet av a, (a och b betraktas här som 1×n-matriser).
I rum av högre dimension än tre, där man inte lika självklart kan tala om längder och vinklar, används det senare ofta som definition av skalärprodukten. Utifrån denna kan man sedan analogt med det plana och det tredimensionella fallet definiera begrepp som längd och vinklar.
Märk särskilt att skalärprodukten är en skalär, ofta ett reellt tal, och inte en vektor - därav dess namn. Ibland används ordet "skalärmultiplikation" i betydelsen multiplikation av en vektor med en skalär, vilket innebär en förväxlingsrisk.