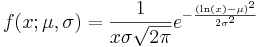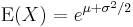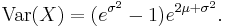Lognormalfördelning
Från Rilpedia
Lognormalfördelningen är en sannolikhetsfördelning som förekommmer inom matematisk statistik. Den beskriver fördelningen för en stokastisk variabel vars logaritm är normalfördelad. Med andra ord, om Y är en normalfördelad stokastisk variabel, så är X = exp(Y) lognormalfördelad.
Definition
En lognormalfördelad stokastisk variabel kan definieras med hjälp av täthetsfunktionen
där μ och σ är parametrar i den normalfördelade stokastiska variabel som ges av logaritmen.
Egenskaper
En lognormalfördelad stokastisk variabel har väntevärde
och varians
Fördelningen har moment av alla ordningar, men ingen momentgenererande funktion. Det gäller också att produkter av oberoende lognormalfördelade stokastiska variabler är lognormalfördelade. Om
är oberoende och lognormalfördelade variabler med samma μ-parameter, men inte nödvändigtvis samma σ, och 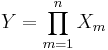 , så är
, så är
 .
.
Däremot är inte summan av oberoende lognormalfödelade stokastiska variabler lognormalfördelad.