Momentgenererande funktion

Från Rilpedia

Texten från svenska Wikipedia

Den momentgenererande funktionen för en stokastisk variabel $X$ definieras som $ψ X (t) = E [e t X]$ , om det 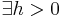$\exists h>0$ så att väntevärdet existerar och är ändligt för $| t | < h$ .

Vidare bestämmer den momentgenererande funktionen unikt fördelningen för stokastiska variabler. Så om två momentgenererande funktioner är lika, $ψ X (t) = ψ Y (t)$ , så har de två stokastiska variablerna, $X$ och $Y$ , lika fördelning.

Man kan visa att om $ψ X (t)$ existerar för $| t | < h$ och något $h > 0$ gäller
a) 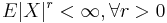$E|X|^r<\infty , \forall r>0$
b) $E[X^n]=\psi^{(n)}_X, n=1,2,...$

Denna artikel i sannolikhetsteori eller statistik är bara påbörjad. Du kan hjälpa till genom att utöka den.

Momentgenererande funktion

Från Rilpedia

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk