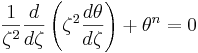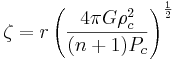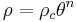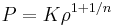Lane-Emdens ekvation

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Lane-Emdens ekvation är inom astrofysiken en poissonekvation för den gravitationella potentialen hos en sfäriskt symmetrisk polytropisk vätska som hålls samman av sin egenskapade gravitation. Ekvationen har fått sitt namn från astrofysikerna Jonathan Homer Lane och Robert Emden. Dess lösning kan användas för att skapa en profil av trycket och densiteten hos vissa sfäriska objekt:

\frac{1}{\zeta^2} \frac{d}{d\zeta} \left({\zeta^2 \frac{d\theta}{d\zeta}}\right) + \theta^n = 0

där

\zeta = r \left(\frac{4 \pi G \rho_c^2}{(n+1)P_c}\right)^{\frac{1}{2}}

och

\rho = \rho_c \theta^n \,

där nedsänkta "c" avser värden av tryck och densitet vid sfärens centrum. Här är n det polytropsika indexet i vilket trycket och densiteten hos en gas förhåller sig genom den polytropiska ekvationen

P = K \rho^{1 + 1/n}\,

Notera att lösningen till Lane-Emden-ekvationen för ett givet polytropiskt indec n är känt som polytroper av index n. Fysiskt kopplar hydrostatisk jämvikt med gradienten hos potentialen, densiteten och gradienten hos trycket, medan Poissons ekvation kopplar potentialen med densiteten. I princip kan vi, om vi vet någonting om gasen mer än sättet trycket och densiteten varierar med avseende till varandra, nå en lösning. Valet av en polytropisk gas som givet ovan gör den matematiska framställningen speciellt koncis, vilket resulterar i Lane-Emden-ekvationen. Detta är en användbar ekvation av "0:e ordning" för en självgravitationell gassfär som stjärnor. Den är fortfarande användbar i vissa situationer, men är vanligen ett ganska begränsande antagande.

Lösningar av ekvationen

Det är känt att ekvationen kan lösas analytiskt när n = 0, 1 eller 5:

n = 0 1 5
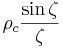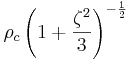ρ = ρc \rho_c \frac{\sin\zeta}{\zeta} \rho_c \left(1+ \frac{\zeta^2}{3}\right)^{-\frac{1}{2}}
ζ = 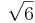\sqrt 6 π ∞

För n = 0 är densiteten konstant och ekvationen reduceras till en sfärisk Bessel-differentialekvation vilken ger en sinc-funktion när n = 1.

Källor

  • Artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia, där angavs (2008-01-15) följande som källor:
  • Lane, Jonathan Homer (1870), "On the Theoretical Temperature of the Sun under the Hypothesis of a Gaseous Mass Maintaining its Volume by its Internal Heat and Depending on the Laws of Gases Known to Terrestrial Experiment", The American Journal of Science and Arts, 2nd series 50: 57–74.
Hämtad från "https://sv.rilpedia.org/wiki/Lane-Emdens_ekvation"
Personliga verktyg