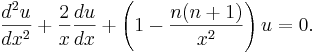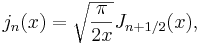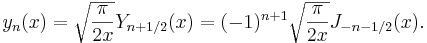Besselfunktion

Texten från svenska Wikipedia

Inom matematiken är besselfunktionerna lösningarna till differentialekvationen

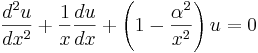$\frac{d^2 u}{dx^2} + \frac{1}{x} \frac{du}{dx} + \left(1 - \frac{\alpha^2}{x^2}\right)u = 0$ .

Denna ekvation uppkommer när man tittar på den radiella delen av Laplaces ekvation i cylindriska koordinater.

Definition

Besselfunktionerna av första slaget definieras av:

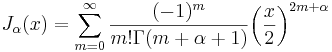$J_\alpha(x) = \sum_{m=0}^\infty \frac{(-1)^m}{m! \Gamma(m+\alpha+1)} {\left({\frac{x}{2}}\right)}^{2m+\alpha}$ .

Differentialekvationen har två linjärt oberoende lösningar och därför behövs även besselfunktioner av andra slaget:

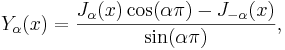$Y_\alpha(x) = \frac{J_\alpha(x) \cos(\alpha\pi) - J_{-\alpha}(x)}{\sin(\alpha\pi)},$ .

$Y α (x)$ är inte begränsad då 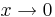$x \to 0$ , vilket gör att man ofta kan bortse från denna lösning av fysikaliska skäl.

I samband med Laplaces ekvation i sfäriska koordinater uppkommer en liknande ekvation för den radiella delen:

$\frac{d^2 u}{dx^2} + \frac{2}{x} \frac{du}{dx} + \left(1 - \frac{n(n+1)}{x^2}\right)u = 0.$

Denna har de sfäriska besselfunktionerna som lösningar.

$j_n(x) = \sqrt{\frac{\pi}{2x}} J_{n+1/2}(x),$

$y_n(x) = \sqrt{\frac{\pi}{2x}} Y_{n+1/2}(x) = (-1)^{n+1} \sqrt{\frac{\pi}{2x}} J_{-n-1/2}(x).$