Polytrop
Från Rilpedia
Polytrop avser inom astrofysiken en lösning till Lane-Emdens ekvation i vilken trycket beror på densiteten i formen P = Kρ((n + 1) / n), där P är tryck, ρ är densitet och K är en konstant. Konstanten n är känd som det polytropiska indexet. Denna koppling behöver inte tolkas som en tillståndsekvation även om en gas som följer en sådan tillståndsekvation producerar en polytropisk lösning till Lane-Emden-ekvationen. Istället är det ett förhållande som uttrycker att antagande gällande utvecklingen av P efter radie, i termer av utvecklingen av P efter radie, vilket ger en lösning till ekvationen.
Ett exempel, med en ideal gas och ett polytropiskt index, är konstanten K
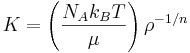
och uttrycket på den högra sidan är antagen vara konstant genom hela lösningen.
En polytrop med index n=0 har en uniform densitet.
Polytroper med ett index mellan ungefär n=0,5 och n=1 kan användas för att skapa goda modeller av neutronstjärnor.
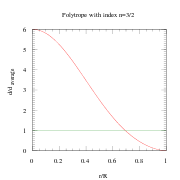
En polytrop med index n=3/2 är en bra modell för degenererade kärnor hos stjärnor och andra stora objekt (till exempel de hos röda jättar, vita dvärgar, bruna dvärgar och även för gasjättar som jupiter och stenplaneter.
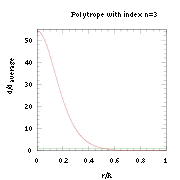
Huvudsekvenstjärnor som solen kan vanligen skapas en model av med en polytrop med index n=3, motsvarande Eddington standard model för strukturen hos stjärnor.
En polytrop med index n=5 har en oändlig radie. Den motsvaras till den enklast tänkbara modellen av ett självöverensstämmande stjärnsystem, som först studerades av Arthur Schuster 1883.
En polytrop med index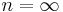 
motsvarar vad som kallas en isoterm sfär som hålls samman av gravitationella krafter och vars struktur är identisk med strukturen hos ett kollisionslöst system av stärnor som en klotformig stjärnhop.
Notera att allt eftersom det polytropiska indexet blir högre ökar koncentrationen av densitetsdistributionen i kärnan.
I vissa fall används termen polytrop för att referera till en tillståndsekvation som påminner om det termodynamiska förhållandet ovan, men detta är potentiellt förvirrande och bör undvikas. Det är fördelaktigt att referera till själva vätskan (till motsatts för lösningen hos Lane-Emden-ekvationen) som en polytropisk vätska. Tillståndsekvationen hos en polytropisk vätska är generellt tillräcklig så att sådana ideala vätskor kan användas även utanför de begränsade problemen av polytroper.
Källor
- Artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia, där angavs (2008-01-15) följande litteratur som källor:
- Chandrasekhar, S. [ 1939 ] ( 1958 ). An Introduction to the Study of Stellar Structure, New York : Dover. ISBN 0-486-60413-6
- Hansen, C.J., Kawaler S.D. & Trimble V. ( 2004 ). Stellar Interiors - Physical Principles, Structure, and Evolution, New York : Springer. ISBN 0-387-20089-4
- Horedt, G.P. ( 2004 ). Polytropes. Applications in Astrophysics and Related Fields, Dordrecht : Kluwer. ISBN 1-4020-2350-2
