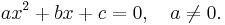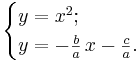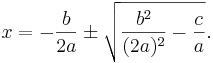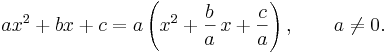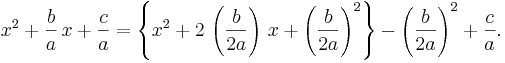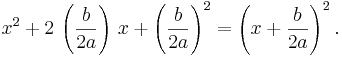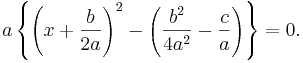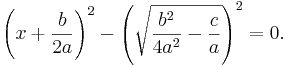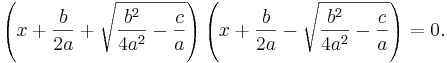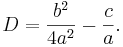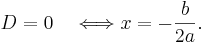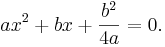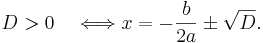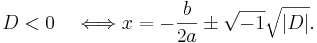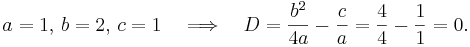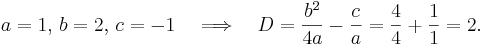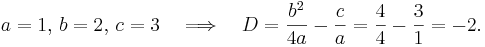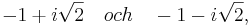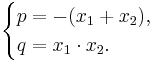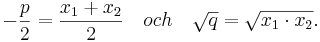Andragradsekvation
Från Rilpedia
Denna artikel behandlar andragradsekvationer med en obekant.
Inom matematiken är en andragradsekvation en ekvation av följande form:
Talen a, b och c är ekvationens koefficienter och uttrycket 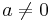 betyder att talet a inte är lika med talet noll. Ordet andragrad- kommer av det faktum att det är talet 2 som är den högsta potensen med vilken det obekanta talet x förekommer i ekvationen. Om den högsta potensen är andra positiva heltal får ekvationen namn därefter; så är exempelvis
betyder att talet a inte är lika med talet noll. Ordet andragrad- kommer av det faktum att det är talet 2 som är den högsta potensen med vilken det obekanta talet x förekommer i ekvationen. Om den högsta potensen är andra positiva heltal får ekvationen namn därefter; så är exempelvis
- x − 1 = 0 en förstagradsekvation;
- x2 − 1 = 0 en andragradsekvation;
- x3 − 1 = 0 en tredjegradsekvation;
- x4 − 1 = 0 en fjärdegradsekvation;
- x5 − 1 = 0 en femtegradsekvation.
Innehåll |
Lösning av ekvationen
Att lösa ekvationen motsvarar att finna skärningspunkterna mellan parabeln y = x2 och den räta linjen y = kx + m, vars lutning k är lika med talet -b/a och som skär y-axeln i punkten (0,m), där talet m = -c/a. Andragradsekvationen kan därför skrivas som ett ekvationssystem:
En andragradsekvation har en eller två lösningar, som är reella eller komplexa tal, beroende på vilka tal som är ekvationens koefficienter:
- Ekvationen x2 + 2x + 1 = 0 har endast en lösning;
- ekvationen x2 + 2x − 1 = 0 har två lösningar som är reella tal;
- ekvationen x2 + 2x + 2 = 0 har två lösningar som är konjugerade komplexa tal.
Ekvationens så kallade diskriminant avgör vilket av de tre fallen som kommer att uppstå. (Se nedan om diskriminanten till en andragradsekvation.)
Lösningsformeln
Formeln
Lösningsformeln för andragradsekvationen ax2 + bx + c = 0 har följande form:
Härledning
Formeln för andragradsekvationens lösningar, eller rötter, kan härledas genom att tillämpa kvadratkomplettering. Först bryts koefficienten a ut:
Sedan kvadratkompletteras uttrycket inom parenteser ovan, genom att lägga till och dra ifrån (b / 2a)2:
Genom att användande av kvadreringsreglerna skrivs uttrycket sedan inom krull-parenteserna {...} som kvadraten av talet x + b / 2a:
Att lösa andragradsekvationen ax2 + bx + c = 0 har nu blivit samma sak som att lösa följande andragradsekvation:
Vi vet att talet a inte är lika med noll, varför uttrycket inom krull-parenteserna {...} måste vara lika med noll:
Med hjälp av konjugatregeln kan vi skriva denna andragradsekvation som två förstagradsekvationer:
Om den första faktorn är lika med noll får vi följande ekvation:
Om den andra faktorn är lika med noll får vi:
Antal rötter
Antalet rötter som andragradsekvationen ax2 + bx + c = 0 har, beror på ekvationens så kallade diskriminant, D, som är det uttryck som står under kvadratrot-symbolen:
En rot
Andragradsekvationen har en rot om, och endast om, diskriminanten är lika med noll:
Villkoret D = 0 kan bara uppfyllas av en speciell sorts andragradsekvation:
Två reella rötter
Andragradsekvationen har två olika rötter som båda är reella tal om, och endast om, diskriminanten är ett positivt tal:
Två komplexa rötter
Andragradsekvationen har två olika rötter som båda är komplexa tal om, och endast om, diskriminanten är ett negativt tal; Vi uttrycker det negativa talet D med hjälp av absolutbelopp-funktionen: 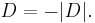
De två rötterna utgör vad som kallas ett komplext konjugat-par, vilket innebär att den ena roten är det motsvarande konjugerade komplexa talet av den andra roten.
Exempel
En rot
Andragradsekvationen x2 + 2x + 1 = 0 har bara en rot, eftersom ekvationens diskriminant är lika med noll:
Roten är talet − 1:
Två reella rötter
Andragradsekvationen x2 + 2x − 1 = 0 har två rötter som båda är reella tal, eftersom ekvationens diskriminant är ett positivt tal:
De båda rötterna är
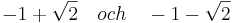 .
.
Två komplexa rötter
Andragradsekvationen x2 + 2x + 3 = 0 har två rötter som båda är komplexa tal, eftersom ekvationens diskriminant är ett negativt tal:
De båda rötterna är det komplexa konjugat-paret
där vi har använt symbolen i för att beteckna den imaginära enheten, 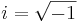 .
.
Samband mellan rötter och koefficienter
Om ekvationen skrivs på formen 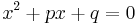 gäller följande samband med dess lösningar, x1 och x2, och dess koefficienter p och q:
gäller följande samband med dess lösningar, x1 och x2, och dess koefficienter p och q:
Talet − p / 2 är därför det aritmetiska medelvärdet av ekvationens lösningar och talet 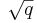 är det geometriska medelvärdet av lösningarna, förutsatt att koefficienten q är ett positivt tal:
är det geometriska medelvärdet av lösningarna, förutsatt att koefficienten q är ett positivt tal:
Härledning
Talen x1 och x2 är rötter till en andragradsekvation om, och endast om, ekvationen kan skrivas som en produkt av två faktorer som båda är av första ordningen:
Om vi utvecklar detta uttryck ser vi sambandet mellan andragradsekvationens koefficienter och dess lösningar: