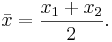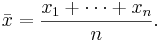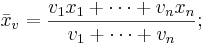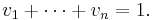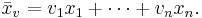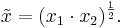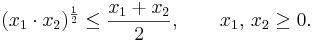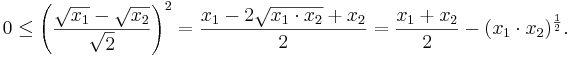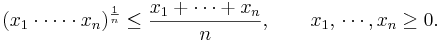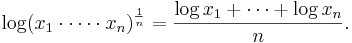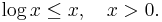Aritmetiskt medelvärde

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Aritmetiskt medelvärde (ofta bara kallat medelvärde) är det genomsnittliga värdet av ett antal tal.

Innehåll

Aritmetiskt medelvärde av två tal

Det aritmetiska medelvärdet av två reella tal, x1 och x2, är det reella tal, 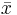\bar x, som ligger mitt emellan de två talen:

\bar x = \frac{x_1+x_2}{2}.

Man kan också uppfatta 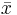\bar x som en tyngdpunkt på följande sätt: Föreställ dig den reella tallinjen som en tunn bräda och placera ut två vikter på platserna x1 och x2; varje vikt väger lika mycket. På platsen 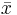\bar x kan vi balansera brädan.

Aritmetiskt medelvärde av fler än två tal

Ovanstående tolkning av det aritmetiska medelvärdet ger oss en känsla för vad medelvärdet av fler än två reella tal är för något: Det aritmetiska medelvärdet av n stycken reella tal x_1, \cdots, x_n är tyngdpunkten för n stycken lika stora vikter utplacerade på platserna x_1, \cdots, x_n:

\bar x = \frac{x_1 + \cdots + x_n}{n}.

Viktat aritmetiskt medelvärde

Om man istället för att placera ut lika tunga vikter på de n platserna lägger ut olika vikter, får man ett så kallat viktat aritmetiskt medelvärde:

\bar x_v = \frac{v_1 x_1 + \cdots + v_n x_n}{v_1 + \cdots + v_n};

På plats x1 placerar vi vikten v1; på plats x2 placerar vi vikten v2, och så vidare. Vi kan utgå ifrån att den sammanlagda vikten är lika med en viktenhet:

v_1 + \cdots + v_n = 1.

Då blir det viktade aritmetiska medelvärdet en så kallad konvex linjärkombination (även kallad konvex kombination) av talen x_1, \cdots, x_n:

\bar x_v = v_1x_1 + \cdots + v_nx_n.

Det aritmetiska medelvärdet är ett exempel på en konvex linjärkombination.

Samband mellan aritmetiskt- och geometriskt medelvärde

Det geometriska medelvärdet mellan två positiva reella tal, x1 och x2, är följande reella tal 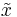\tilde x:

\tilde x = (x_1 \cdot x_2)^{\frac{1}{2}}.

Med hjälp av den så kallade kvadreringsregeln från algebran kan vi visa att det geometriska medelvärdet av två positiva tal aldrig kan vara större än det aritmetiska medelvärdet av talen:

(x_1 \cdot x_2)^{\frac{1}{2}} \leq \frac{x_1+x_2}{2}, \qquad x_1, \, x_2\geq 0.

Härledning av sambandet för två positiva tal

Vi tillämpar kvadreringsregeln på det speciella uttrycket 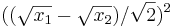((\sqrt{x_1}-\sqrt{x_2})/\sqrt{2})^2 och noterar att detta tal alltid är positivt:

0 \leq \left( \frac{ \sqrt{x_1} - \sqrt{x_2} }{ \sqrt{2} } \right)^2 = \frac{x_1 - 2\sqrt{x_1\cdot x_2} + x_2}{2} = \frac{x_1+x_2}{2} - (x_1 \cdot x_2)^{\frac{1}{2}}.

Vi ser också att de aritmetiska och geometriska medelvärdena är lika stora om, och endast om, x1 och x2 är samma tal.

Utvidgning av sambandet till fler än två positiva tal

Genom att använda tekniken matematisk induktion, kan man visa att olikheten mellan aritmetiskt och geometriskt medelvärde gäller även då man har fler än två positiva tal:

(x_1 \cdot \cdots \cdot x_n)^{\frac{1}{n}} \leq \frac{x_1 + \cdots + x_n}{n}, \qquad x_1, \, \cdots, x_n \geq 0.

Logaritmfunktionen visar att det geometriska medelvärdet är ett slags aritmetiskt medelvärde:

\log(x_1 \cdot \cdots \cdot x_n)^{\frac{1}{n}} = \frac{\log x_1 + \cdots + \log x_n}{n}.

Olikheten mellan det aritmetiska- och det geometriska medelvärdet kommer då från följande olikhet för logaritmfunktionen:

\log x \leq x, \quad x > 0.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Aritmetiskt_medelv%C3%A4rde"
Personliga verktyg