Kommutativitet
Från Rilpedia
Kommutativitet är ett begrepp inom matematiken, speciellt inom abstrakt algebra, som egenskap hos en binär operator.
Operatorn  på en mängd S är kommutativ om och endast om det för alla x och y i S gäller att
på en mängd S är kommutativ om och endast om det för alla x och y i S gäller att
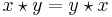 .
.
Operatorn är alltså kommutativ om det inte spelar något roll i vilken ordning man utför operationen. De mest kända exemplen på kommutativa operatorer är addition och multiplikation av naturliga tal, till exempel:
- 4 + 5 = 5 + 4 (eftersom båda uttrycken ger 9)
- 2 · 3 = 3 · 2 (eftersom båda uttrycken ger 6)
Exempel på icke kommutativa operationer är
- subtraktion: 5 - 4=1 ≠ 4 - 5=-1 (subtraktion är dock antikommutativ, se nedan)
- potens: 25 = 32 ≠ 52 =25
Ytterligare exempel på kommutativa binära operatorer inkluderar addition och multiplikation av reella tal och komplexa tal, addition av vektorer, samt snitt och unioner av mängder. Viktiga operatorer som generellt är ickekommutativa är multiplikation av matriser, sammansättning av funktioner och kvaternionmultiplikation.
Innehåll |
Kommutativitet och algebraiska strukturer
En abelsk grupp definieras som en grupp (en mängd där (endast) en operation, till exempel addition eller multiplikation, behöver vara definierad) vars operator är kommutativ. Abelsk grupp och kommutativ grupp är alltså synonymer.
En ring (en mängd där likt de reella talen två sammanhängande operationer, motvarande addition och multiplikation) kallas kommutativ om dess multiplikation är kommutativ, eftersom addition alltid är kommutativ, genom hur man definierat ring. Slutligen definieras en kropp (engelska field), som en kommutativ ring, där varje element skilt från det additiva identitetselementet har multiplikativ invers.
Antikommutativitet
En antikommutativ binär operator  på en ring uppfyller
på en ring uppfyller 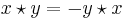 för alla x och y. Det är först svårt att föreställa sig någon naturligt förekommande antikommutativ operator, när man tänker på och jämför med addition och multiplikation av reella tal. Standardexemplet, med rötter i elektromagnetismen, är kryssprodukten
för alla x och y. Det är först svårt att föreställa sig någon naturligt förekommande antikommutativ operator, när man tänker på och jämför med addition och multiplikation av reella tal. Standardexemplet, med rötter i elektromagnetismen, är kryssprodukten  . Den visar i vilken riktning kraften blir på en strömförande ledare, givet strömriktningen och ett yttre magnetfälts riktning:
. Den visar i vilken riktning kraften blir på en strömförande ledare, givet strömriktningen och ett yttre magnetfälts riktning:
där F är kraften, B magnetfältet och I strömmen. Kryssprodukter används också för att beräkna vridmoment.
Antikommutativa operatorer används också inom kvantmekaniken för att beskriva elektroner och andra så kallade fermioniska partiklar som lyder under Paulis uteslutningsprincip.
Kommutator
En kommutator i en grupp är ett element som kan skrivas på formen
för några element a och b i gruppen. Enhetselementet e kan alltid skrivas som
och därför är alltid e en kommutator i varje grupp, abelsk såväl som icke-abelsk. Man kan därför säga att intressanta egenskaper hos grupper uppstår först när man har andra kommutatorer än enhetselementet e.
Observera att om operatorn  är kommutativ, så reduceras varje kommutator till enhetselementet e. Det beror på att man kan då skriva
är kommutativ, så reduceras varje kommutator till enhetselementet e. Det beror på att man kan då skriva
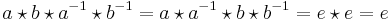 .
.
eftersom det bara är att byta ordningen på operanderna i en kommutativ grupp. Därför kan man säga att det är ointressant studera kommutatorer i kommutativa grupper, man vet ju redan precis hur de ser ut: de är alla enheten e.
Kommutator-undergruppen K till en grupp G är mängden av alla kommutatorer till gruppen. Den bildar en normal undergrupp till ursprungsgruppen G och då blir kvotgruppen G / K också kommutativ.
Löst uttryckt kan man därför säga att kvotgruppen G / K (men även kommutatorundergruppen K) ger värdefull information om ursprungsgruppen G, till exempel vilken struktur den har, trots att kvotgruppen oftast bara utgör en liten del av ursprungsgruppen. Det beror på att man reducerat problemet att finna egenskaper hos en icke-kommutativ grupp till en som är kommutativ. På köpet brukar kvotgruppen bli betydligt mindre och inte så oöverskådlig som ursprungsgruppen möjligen var, vilket kan vara fördelaktigt. Matematiken förstår generellt sett kommutativa grupper bättre än icke-kommutativa, se struktursatsen för abelska grupper, och mindre grupper bättre än större.
Kommutatorn i en ring definieras för två element A och B via så kallade Poisson-hakar genom relationen:
och är därmed en antikommutativ binär operator. Man ser att om vi kan kasta om ordningen hos operatorn  kommer kommutatorn bli noll. Den används i fysik till exempel för att studera kvantmekaniska invarianter. Den är närbesläktat med abstrakt algebraiska begrepp som centre och centralizer.
kommer kommutatorn bli noll. Den används i fysik till exempel för att studera kvantmekaniska invarianter. Den är närbesläktat med abstrakt algebraiska begrepp som centre och centralizer.
På liknande sätt definieras antikommutatorn {A,B} = A B + B
B + B A
A




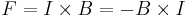
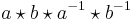
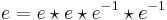
![[A,B] = A \star B - B \star A](/w/images/sv.rilpedia.org/math/1/9/5/195cde16c0f6b124bb85c6d4a1d5930d.png)