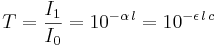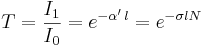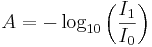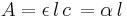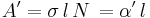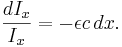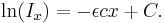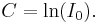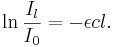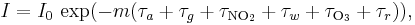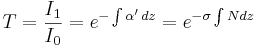Beers lag
Från Rilpedia
Beers lag, också kallad Beer-Lamberts lag eller Beer-Lambert-Bougers lag är i optiken ett samband mellan absorptionen (dämpningen) av elektromagnetisk strålning och egenskaperna hos det material genom vilket den passerar.
Innehåll |
Sambandet
Lagen anger att det finns ett exponentiellt samband mellan transmissionen av ljus  genom substansen och produkten av absorbansen
genom substansen och produkten av absorbansen 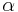 och den väg ljuset passerar genom materialet,
och den väg ljuset passerar genom materialet, 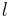 . Absorbansen kan i sin tur skrivas som en produkt av antingen
. Absorbansen kan i sin tur skrivas som en produkt av antingen 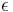 , den molära absorptiviteten för substansen och den molära koncentrationen av substansen i materialet,
, den molära absorptiviteten för substansen och den molära koncentrationen av substansen i materialet, 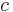 , eller alternativt ett absorptionstvärsnitt
, eller alternativt ett absorptionstvärsnitt 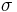 , och tätheten av den absorberande substansen i materialet
, och tätheten av den absorberande substansen i materialet 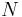 (i antal partiklar per volymsenhet).
(i antal partiklar per volymsenhet).
Vid arbete i lösningar i vätska skrivs detta vanligen:
medan fysiker för spektroskopi och spektrofotometri i gaser vanligen skriver dem:
där 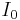 och
och 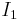 är ljusintensiteten för det ingående ljuset och ljusintensiteten hos det utgående ljuset, respektive.
är ljusintensiteten för det ingående ljuset och ljusintensiteten hos det utgående ljuset, respektive.
Ur ljustransmissionen kan vi definiera absorbansen
medan den av fysiker i gaser i allmänhet definieras
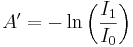 .
.
Härav följer att absorbansen är proportionell mot koncentrationen (eller tätheten av absorberande enheter) enligt sambandet
och
för de två fallen.
Om man därför känner väglängden och den molära extinktionskoefficienten (eller absorptionstvärsnittet) och mäter absorbansen kan koncentrationen av substansen beräknas.
Dessa sista två är de samband som bör gå under beteckningen Lambert-Beers lag. Orsaken är att historiskt sett Lambert härledde den lag som säger att absorbansen är proportionell mot väglängden, medan Beer är upphovsman till sambandet att den är proportionell mot koncentrationen.[1]
Om koncentrationen uttrycks som molbråk, d v s en sortlös storhet får absorbansen (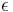 ) samma dimension som extinktionskoefficienten, d v s invers längdskala (t ex m−1 eller cm-1). Om koncentrationen uttrycks i mol per volymsenhet blir extinktionskoefficienten(
) samma dimension som extinktionskoefficienten, d v s invers längdskala (t ex m−1 eller cm-1). Om koncentrationen uttrycks i mol per volymsenhet blir extinktionskoefficienten(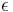 ) uttryckt i L·mol−1·cm−1, eller i andra enheter i mol−1 cm2.
) uttryckt i L·mol−1·cm−1, eller i andra enheter i mol−1 cm2.
Det finns alltså två olika definitioner på absorbansen (baserade på 10 respektive e) vilket innebär att extinktionskoefficienten när det gäller gaser 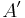 och
och 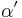 , är ln 10 (ungefär 2,3) gånger högre än den för vätskor
, är ln 10 (ungefär 2,3) gånger högre än den för vätskor 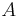 och
och 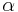 , respektive. Man måste därför vara försiktig när man tillämpar lagen så att den riktiga formen av lagen används.
, respektive. Man måste därför vara försiktig när man tillämpar lagen så att den riktiga formen av lagen används.
Härledning
Antag att ljuset passerar genom materialet i x-riktningen. I punkten x har ljuset intensiteten Ix. Vid passagen genom den (infinitsimala) skivan dx ändras intensiteten dI:
Integrering av båda sidor ger:
Det ingående ljusets intensitet är I0 vid x=0. Insättning ger integrationskonstantens värde:
Förutsättningar
Fem förutsättningar måste vara uppfyllda för att denna lag skall vara giltig:
- Molekylerna i lösningen måste vara oberoende av varandra. Om färgade molekyler binds till varandra med bildning av komplex med andra optiska egenskaper ger detta olinearitet.
- Mediet i strålens väg måste vara homogent och det får inte sprida ljuset.
- Ljusstrålen måste vara parallell, och alla vägar ljuset kan ta genom mediet måste vara lika långa,
- Ljuset måste vara monokromatiskt eller åtminstone ha så liten bandbredd att det absorberande ämnets absorbans inte ändras påtagligt inom ljusstrålens bandbredd.
- Ljuset får inte påverka molekylerna. Det får alltså inte bryta ned molekylerna eller pumpa upp dem så att en avsevärd mängd ligger på en högre energinivå eftersom detta skulle förändra koncentrationen av molekyler på lägsta energinivån och till och med kunna ge upphov till stimulerad ljusemission.
Om någon av dessa betingelser inte är uppfylld erhålls avvikelser från Beers lag.
Kemisk och klinisk analys
Beers lag kan användas för analys av blandningar av substanser, också av olika färgade substanser, genom spektrofotometri. Om man har flera färgade substanser närvarande måste man mäta vid olika våglängder, där förhållandet mellan ämnenas extinktionskoefficienter är olika. Man kan då ställa upp ekvationssystem där substanserna antas ge sina bidrag till den totala absorbansen oberoende av varandra.
En viktig tillämpning är mätningen av p-nitrofenol i alkalisk lösning. Föreningar av p-nitrofenol är färglösa. Detta gäller t ex p-nitrofenylfosfat. Därför används ofta alkaliskt fosfatas som en markör i immunkemiska bestämningar. Under reaktionen binds markören (tracer), och efter den immunkemiska reaktionen kan det alkaliska fosfatas som är kvar i lösning tvättas bort. En lösning av p-nitrofenylfosfat i alkalisk lösning sätts till och får reagera en bestämd tid. Fosfataset bryter ned p-nitrofenylfosfatet till fosfat och p-nitrofenyljoner, som har intensivt gul färg. Reaktionen bryts efter en bestämd tid och den uppkomna gula färgen mäts vid våglängden 405 nm. Också andra föreningar med p-nitrofenylfosfat används, t ex galaktosiden av p-nitrofenylfosfat för att mäta aktiviteten av 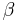 -galaktosidas.
-galaktosidas.
Beers lag i atmosfären
Lagen används också för att beskriva dämpningen av ljuset från sol eller stjärnor då det färdas genom atmosfären. I detta fall måste man ta hänsyn till spridning förutom absorption. För ljusets dämpning i atmosfären skrivs Beers lag ofta:
där varje τx är det optiska djup som definieras av motsvarande index. Det optiska djupet definieras som negativa logaritmen för den del av ljuset som sprids eller absorberas bort under vägen.
- a hänför sig till aerosoler som sprider och absorberar strålning,
- g hänför sig till homogent blandade gaser (huvudsakligen koldioxid (CO2) och syre (O2) vilka endast absorberar)
- NO2 hänför sig till kvävedioxid, huvudsakligen från utsläpp, vilket endast absorberar
- w hänför sig till vattenånga, vilket absorberar
- O3 hänför sig till ozon vilket absorberar
- r hänför sig till Rayleigh-spridning från syre (O2) och kväve (N2) (vilken ger himlen dess blå färg).
m är den optiska massan or luftmassan, en term som vid låga och moderata värden ger θ ungefär lika med 1 / cos(θ), där θ är det observerade objektets zenitvinkel (vinkeln mellan riktningen till det observerade objektet och en linje vinkelrät mot jordytan vid observationsstället).
Denna ekvation kan användas för att beräkna τa, det optiska djupet för aerosoler, vilket krävs för korrektion av satellitbilder och som också är viktigt för beräkning av aerosolernas betydelse för klimatet.
Vid beräkning av ljusets väg genom atmosfären är denna inte homogen, utan man måste föra in följande korrektion:
där z är längden av ljusets väg genom atmosfären, övriga symboler de som angivits ovan[2]. Hänsyn har tagits till detta i varje τx i atmosfärekvationen ovan.
Historia
Lagen upptäcktes av Pierre Bouguer före 1729. Den hänförs ofta till Johann Heinrich Lambert, som citerade Bouguers “Essai d'Optique sur la Gradation de la Lumiere” (Claude Jombert, Paris, 1729) — och också citerade från den — i sitt verk “Photometria” 1760. Mycket senare utvidgade den tyske matematikern och fysikern August Beer till att innefatta koncentrationen av den absorberande substansen.
Se också
(Redigerad med utgångspunkt från motsvarande artikel i engelska Wikipedia)
Externa länkar
References
- ↑ J. D. J. Ingle and S. R. Crouch, Spectrochemical Analysis, Prentice Hall, New Jersey (1988)
- ↑ ISBN 0521339561 Houghton, J.T. The Physics of Atmospheres 2nd ed. Chapter 2