Vektor
Från Rilpedia
- Denna artikel handlar om det matematiska begreppet vektor. Se även vektor (olika betydelser).
| Matematiska begrepp |
|---|
Vektorer avser oftast det som används bl.a. i fysiken för att räkna med exempelvis krafter, hastigheter och acceleration, det vill säga storheter som har både längd (magnitud) och riktning. Sådana vektorer kan även kallas rumsvektorer eller geometriska vektorer.
Inom matematiken kan vektorer generaliseras till att vara element i ett vektorrum av godtycklig dimension. En sådan generaliserad vektor har ändå en så kallad norm som anknyter till längdbegreppet. Vektorer kan också bli parallella eller ortogonala, vilket visar att de har riktning i någon mening. Med denna definition anses många typer av objekt vara vektorer. Det enda kravet är att de följer alla de räknelagar som gäller för rumsvektorer.
Innehåll |
Definition och skrivsätt
En vektor är ett matematiskt objekt som karaktäriseras av att det har både längd och riktning. En vektor kan skrivas som en linjärkombination av komponenter, som multiplicerade med sin respektive enhetsvektor blir komposanter. En vektor skrivs ofta genom att man skriver namnet på vektorn och ritar en pil eller ett streck över namnet. (I tryck är det också vanligt att man skriver vektorer med fet stil.)
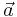 eller
eller 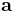
Vektorer i det reella tvådimensionella planet R2
En vektor har som sagt både längd och riktning. Detta kan anges på två olika sätt. Om man till exempel har en vektor med längden 5 och en riktning som lutar 45 grader i förhållande till x-axeln så skriver man:
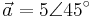
Men när man ska räkna med flera vektorer samtidigt är denna notation opraktisk. Det finns därför en annan notation, kallad matrisform. Här uppfattar man vektorn som hypotenusan i en rätvinklig triangel och anger hur långt den når i x-axelns riktning och hur långt den når i y-axelns riktning.
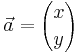
Detta kan också skrivas som en radvektor istället för en kolumnvektor:
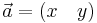
Om man har en vektor som skrivits med vinkel och längd och vill skriva om den på matris-form gör man så här:
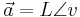
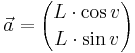
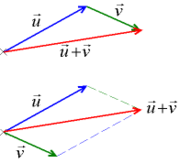
Addition av vektorer
När man lägger ihop två vektorer (till exempel för att beräkna två samverkande krafters totala resulterande kraft) får man en ny vektor, den så kallade summa-vektorn. Om man har de två vektorerna:
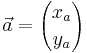
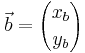
kan man beräkna summan 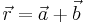 av dem på följande sätt:
av dem på följande sätt:
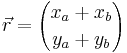
Om man har tre eller flera vektorer kan man lägga samman dem efter samma princip (x-koordinaterna summeras för sig och y-koordinaterna summeras för sig).
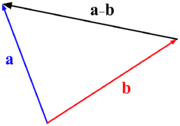
Subtraktion av vektorer
Vektorer dras ifrån varandra efter samma princip som man lägger samman dem. Dock uppfattar man vektorers differens som:
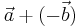
Att man skriver 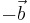 betyder helt enkelt att vektorn vänds och alltså riktas åt motsatt håll. Det uppfattas också som:
betyder helt enkelt att vektorn vänds och alltså riktas åt motsatt håll. Det uppfattas också som:
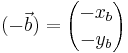
Men detta görs endast grafiskt. Analytiskt drar man vektorer från varandra genom att säga:
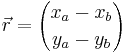
Multiplikation av vektorer
Det finns två olika varianter av multiplikation mellan två vektorer, skalärprodukt och kryssprodukt. Skalärprodukten är en skalär, ett ensamt talvärde som blir störst när vektorerna är parallella. En kryssprodukt är en ny vektor som är vinkelrät mot båda vektorerna som multipliceras, men som blir noll när vektorerna är parallella. Begreppet vektorprodukt används bara om operationer som ger en vektor som resultat. Alltså är kryssprodukten men inte skalärprodukten en vektorprodukt.
Division av vektorer
Någon operator som skulle kunna sägas dividera två vektorer finns inte. Detta beror på att vektorer kan ses som icke-kvadratiska matriser: för sådana existerar ingen multiplikativ invers.
Skalning av en vektor
När man vill ändra en vektors längd multiplicerar man x-koordinaten och y-koordinaten med skalfaktorn. Formeln är:
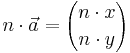
Vektorers längd
När man har skrivit en vektor i matris-form finns ett ganska lätt sätt att beräkna dess längd. Eftersom man kan uppfatta en vektor som hypotenusan i en rätvinklig triangel, kan man använda Pythagoras sats. En vektors längd skrivs alltså som:
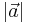
Formeln för vektorns längd är då:
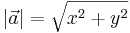
Vektorer i R3
Om vektorrummet är tredimensionellt, dvs. om man har tre riktningar x,y,z, så har vektorerna också tre komponenter. Det tvådimensionella planet 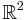 kan ses som ett plan i
kan ses som ett plan i 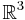 som man får genom att sätta z-komponenten till 0. De flesta formler ovan ändras då på det förväntade sättet. Till exempel skriver man
som man får genom att sätta z-komponenten till 0. De flesta formler ovan ändras då på det förväntade sättet. Till exempel skriver man
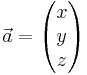
och längden av denna vektor beräknas som
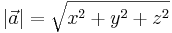
Vektorvärda storheter
Många fysikaliska storheter uttrycks som vektorer. Dit hör bl a hastighet, acceleration, kraft, rörelsemängd, elektriskt fält och magnetfält.
Se även
 Wikimedia Commons har media som rör Vektor
Wikimedia Commons har media som rör Vektor